Persamaan Linear Dua Variabel, SPLDV Substitusi, Eliminasi, & Campuran

A. Pengertian Sistem Persamaan Linear Dua Variabel (SPLDV) 

Sistem persamaan linear dua variabel adalah beberapa bentuk persamaan yang terdiri dari dua variabel (PLDV) dan saling berkaitan dalam sistem linear untuk mengubah suatu pernyataan matematis ke bentuk persamaan sederhana. Sistem ini sering disebut dengan SPLDV atau dalam bahasa inggris "System of Linear Equations in Two Variables".

Sistem persamaan linear dua variabel (SPLDV) merupakan peningkatan dari sistem persamaan linear satu variabel (SPLSV) untuk memecahkan masalah yang lebih kompleks. Minimal terdapat 2 bentuk persamaan linear dua variabel (PLDV) untuk membentuk sistem persamaan linear dua variabel (SPLDV) sebagai teknik pemecahan kasus matematika. Sebelum mempelajari SPLDV, dibutuhkan pemahaman materi terkait SPLSV. 

Artikel terkait: Sistem Persamaan Linear Satu Variabel (SPLSV)

Navigasi Cepat:

• A. Pengertian SPLDV
  • A1. Bentuk Umum PLDV dalam SPLDV
  • A2. Contoh Bentuk Umum PLDV
• B. Cara Penyelesaian SPLDV
  • B1. Metode Substitusi SPLDV dan Contoh
  • B2. Metode Eliminasi SPLDV dan Contoh
  • B3. Metode Campuran SPLDV dan Contoh
• C. Contoh Soal Cerita SPLDV

A1. Bentuk Umum Persamaan Linear Dua Variabel dalam SPLDV

Beberapa persamaan linear dua variabel (PLDV) yang saling berkaitan membentuk sistem persamaan linear dua variabel (SPLDV) yang dapat digunakan sebagai teknik pemecahan suatu kasus matematika. Berikut bentuk umum dan ciri-ciri sistem persamaan linear dua variabel.

ax + by + c = 0

dengan:

• x dan y merupakan 2 variabel pada persamaan
• a merupakan koefisien variabel x
• b merupakan koefisien variabel y
• c merupakan konstanta pada ruas kiri
• Konstanta 0 pada salah satu ruas merupakan bentuk solusi umum dari fungsi persamaan linear (sebagai konsep dasar). Namun, tidak semua persamaan linear ditulis seperti ini.

Catatan: Bentuk umum suatu fungsi persamaan adalah ekuivalen dengan 0 atau "Zero of Function". Pemahaman ini akan digunakan di tingkat pembelajaran yang lebih tinggi.

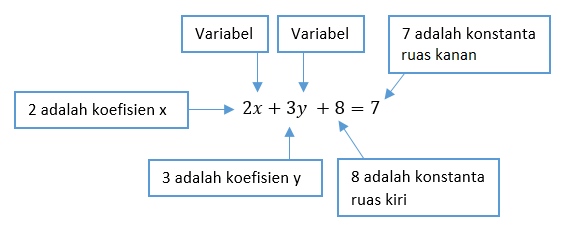
A2. Contoh Bentuk Umum PLDV dan Elemen Pembentuknya

Berikut contoh persamaan linear dua variabel (PLDV) dan elemen pembentuknya.

Alasan: Persamaan "2x + 3y + 8 = 7" merupakan bentuk persamaan linear dua variabel (PLDV) karena mempunyai dua variabel yaitu x dan y.

---

B. Cara Penyelesaian SPLDV dan Contoh Soal

Terdapat 3 cara untuk penyelesaian sistem persamaan linear dua variabel (SPLDV) yaitu dengan metode substitusi, eliminasi, dan campuran.

B1. Metode Substitusi (Menggabungkan)

Metode substitusi adalah metode yang digunakan untuk penyelesaian bentuk aljabar dengan menggabungkan persamaan-persamaan yang telah diketahui menjadi suatu kesatuan. Dalam penyelesaian SPLDV diperlukan minimal 2 persamaan untuk menemukan solusi masing-masing variabel.

Contoh Penyelesaian SPLDV dengan Metode Substitusi

Tentukan nilai variabel x dan y dari persamaan berikut menggunakan metode substitusi

2x + 4y = 28 ... (i)
3x + 2y = 22 ... (ii)

Penyelesaian:

1# Memilih salah satu persamaan yang akan dipindahkan salah satu variabel-nya

Hal pertama yang dilakukan saat menggunakan metode substitusi yaitu memilih salah satu persamaan untuk dipindahkan elemen-nya. Disarankan memilih persamaan yang paling mudah, sehingga tidak menghasilkan angka desimal saat langkah berikutnya. Untuk beberapa kasus setiap persamaan mungkin mempunyai tingkat kesulitan yang sama, yaitu sama-sama menghasilkan angka desimal. Jadi, pemilihan persamaan bersifat bebas dan relatif.

Misalnya dipilih persamaan (i) yaitu 2x + 4y = 28

2# Memindahkan salah satu variabel pada persamaan yang dipilih

Misalnya, dipilih variabel y untuk dipindahkan ke ruas kanan, 

   2x + 4y = 28 ... (i)
⇔ 2x = 28 - 4y 

Karena, dipilih variabel y untuk dipindahkan, sehingga diperoleh bentuk solusi untuk variabel x, yaitu menghilangkan koefisien x dengan membagi masing-masing ruas dengan nilai koefisien x,  

 2x  =  28 - 4y 
 2         2
⇔ x = 14 - 2y ... (iii)

Sehingga ditemukan persamaan (iii) bentuk solusi dari variabel x

3# Menggabungkan persamaan (iii) pada persamaan yang tidak dipilih di awal (ii) untuk menghitung solusi numerik variabel lainnya

3x + 2y = 22 ... (ii)

Karena diperoleh bentuk solusi x pada persamaan (iii),

x = 14 - 2y ... (iii)

Selanjutnya gabungkan dengan cara mengganti variabel x sebagai bentuk solusinya pada persamaan (ii),

   3     x     + 2y = 22
⇔ 3 (14 - 2y) + 2y = 22
⇔ 42 - 6y + 2y = 22
⇔ 42 - 4y = 22
⇔ -4y = 22 - 42
⇔ -4y = -20
⇔  -4y  =  -20 
    -4      -4
⇔ y = 5

Sehingga, diperoleh solusi variabel y = 5

4# Menghitung solusi numerik variabel lain

Karena sudah ditemukan solusi variabel y = 5, dapat dihitung dengan menggabungkan y = 5 pada bentuk solusi x pada persamaan (iii) 

   x = 14 - 2y ... (iii)
⇔ x = 14 - 2(5)
⇔ x = 14 - 10
⇔ x = 4

Sehingga, diperoleh solusi variabel x = 4

Jawaban: Solusi SPLDV tersebut adalah x = 4 dan y = 5

Untuk memastikan jawaban tersebut benar, perlu diuji dengan memasukkan nilai x = 4 dan y = 5 pada soal

2x + 4y = 28 ... (i) 
2(4) + 4(5) = 28
8 + 20 = 28 (Benar)

3x + 2y = 22 ... (ii)
3(4) + 2(5) = 22
12 + 10 = 22 (Benar)

B2. Metode Eliminasi (Menghilangkan)

Metode eliminasi adalah metode yang digunakan untuk penyelesaian bentuk aljabar dengan menghilangkan salah satu variabel untuk menentukan solusi variabel lainnya. Dalam penyelesaian SPLDV diperlukan minimal 2 persamaan untuk menemukan solusi masing-masing variabel.

Contoh Penyelesaian SPLDV dengan Metode Eliminasi

Tentukan nilai variabel x dan y dari persamaan berikut menggunakan metode eliminasi

 x + 2y = 20
2x + 3y = 33

Penyelesaian:

1# Menghitung solusi variabel x

Untuk menghitung solusi variabel x menggunakan metode eliminasi, diperlukan menghilangkan variabel y pada masing-masing persamaan.

 x + 2y = 20
2x + 3y = 33 _

Koefisien variabel y pada masing-masing persamaan adalah 2 dan 3
Hitung KPK dari 2 dan 3

2y → 2, 4, 6, 8, ... 
3y → 3, 6, 9, ...

KPK 2 dan 3 adalah 6, hitung pengali masing-masing koefisien sehingga menghasilkan nilai 6

2 → 6 : 2 = x3
3 → 6 : 3 = x2

Kemudian, lakukan eliminasi dengan menggunakan nilai masing-masing pengali

 x + 2y = 20   | x3
2x + 3y = 33 _ | x2

Diperoleh:

3x + 6y = 60   
4x + 6y = 66 _
-x      = -6
x       =  6

Mengapa ini terjadi?
Perhatikan elemen -x mempunyai nilai koefisien -1 (koefisien 1 dalam penulisan biasanya tidak ditulis, sehingga ditulis tanda "minus" saja)
 -x = -6
 -1   -1

Ingat, bentuk pecahan sama dengan operasi pembagian
-1x : -1 = 1x = x
-6  : -1 = 6
#Tips Negatif : Negatif = Positif

Diperoleh
x = 6

Sehingga diperoleh solusi variabel x = 6

Baca juga: Cara menghitung KPK dan FPB

2# Menghitung solusi variabel y

Untuk menghitung solusi variabel y menggunakan metode eliminasi, diperlukan menghilangkan variabel x pada masing-masing persamaan.

 x + 2y = 20 
2x + 3y = 33 _ 

Koefisien variabel x pada masing-masing persamaan adalah 1 dan 2
Hitung KPK dari 1 dan 2

x  → 1, 2, 3, ...
2x → 2, 4, 6, ...

KPK 1 dan 2 adalah 2, hitung pengali masing-masing koefisien sehingga menghasilkan nilai 2

1 → 2 : 1 = x2 
2 → 2 : 2 = x1

Kemudian, lakukan eliminasi dengan menggunakan nilai masing-masing pengali 

 x + 2y = 20   | x2
2x + 3y = 33 _ | x1 

Diperoleh:

2x + 4y = 40  
2x + 3y = 33 _
      y = 7

Sehingga diperoleh solusi variabel y = 7 

Jawaban: Solusi SPLDV tersebut adalah x = 6 dan y = 7

Untuk memastikan jawaban tersebut benar, perlu diuji dengan memasukkan nilai x = 6 dan y = 7 pada soal

x + 2y = 20 
(6) + 2(7) = 20
6 + 14 = 20 (Benar)

2x + 3y = 33
2(6) + 3(7) = 33
12 + 21 = 33 (Benar)

B3. Metode Campuran (Hybrid Eliminasi dan Substitusi)

Metode campuran adalah metode hybrid (gabungan) dari metode eliminasi dan metode substitusi untuk mencari solusi persamaan bentuk aljabar. Metode campuran merupakan alternatif untuk menghasilkan perhitungan yang lebih cepat. Cara kerja metode ini yaitu melakukan eliminasi untuk mencari solusi suatu variabel, lalu melakukan substitusi variabel yang telah ditemukan untuk menghitung variabel berikutnya.

Contoh Penyelesaian SPLDV dengan Metode Campuran

Tentukan nilai variabel x dan y dari persamaan berikut menggunakan metode campuran

2x + 3y = 8
5x + 7y = 19

Penyelesaian:

#1 Langkah Eliminasi

Misalnya langkah pertama mencari solusi variabel x dengan eliminasi variabel y pada masing-masing persamaan

2x + 3y = 8
5x + 7y = 19 _

Koefisien variabel y pada masing-masing persamaan adalah 3 dan 7
Hitung KPK dari 3 dan 7

3y → 3, 6, 9, 12, 15, 18, 21, 24, ...
7y → 7, 14, 21, 28, ...

KPK 3 dan 7 adalah 21, hitung pengali masing-masing koefisien sehingga menghasilkan nilai 21

3 → 21 : 3 = x7
7 → 21 : 7 = x3

Kemudian, lakukan eliminasi dengan menggunakan nilai masing-masing pengali

2x + 3y = 8    | x7
5x + 7y = 19 _ | x3

Diperoleh:

14x + 21y = 56
15x + 21y = 57 _
 -x       = -1
  x       =  1

Sehingga ditemukan solusi variabel x = 1

#2 Langkah Substitusi

Karena solusi variabel x telah ditemukan, dilanjutkan dengan substitusi ke salah satu persamaan pada soal (bebas). 

Misalnya dipilih persamaan pertama soal

2x + 3y = 8

dengan substitusi x = 1 diperoleh,

⇔ 2(1) + 3y = 8
⇔ 2 + 3y = 8
⇔ 3y = 8 -2
⇔ 3y = 6
⇔  y = 2

Sehingga ditemukan solusi variabel y = 2

Jawaban: Solusi SPLDV tersebut adalah x = 1 dan y = 2

Untuk memastikan jawaban tersebut benar, perlu diuji dengan memasukkan nilai x = 1 dan y = 2 pada soal

2x + 3y = 8
2(1) + 3(2) = 8
2 + 6 = 8 (Benar)

5x + 7y = 19
5(1) + 7(2) = 19
5 + 14 = 19 (Benar)

---

C. Contoh Soal Cerita SPLDV

Andi and Budi membeli alat-alat tulis di sebuah toko. Andi membeli 2 buku dan 3 pulpen dengan harga Rp 17.000,- dan Budi membeli 1 buku dan 10 pulpen dengan harga Rp 34.000,- 

Berapakah harga sebuah buku dan sebuah pulpen?

Penyelesaian:

Dari soal di atas dapat dibentuk persamaan SPLDV, sebagai berikut.

Dengan mendefinisikan:
Buku sebagai variabel x
Pulpen sebagai variabel y

Dapat dibentuk SPLDV berikut, 

2 Buku + 3 Pulpen = Rp 17.000,-
1 Buku + 10 Pulpen = Rp 34.000,-

2x + 3y = 17.000
x + 10y = 34.000

Untuk mempermudah penyelesaian, akan digunakan metode campuran

#1 Langkah Eliminasi

Pada langkah ini dihitung solusi x dengan eliminasi variabel y

2x + 3y = 17.000
x + 10y = 34.000

Koefisien variabel y pada masing-masing persamaan adalah 3 dan 10
Hitung KPK dari 3 dan 10

 3y → 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, ...
10y → 10, 20, 30, 40, ...

KPK 3 dan 10 adalah 30, hitung pengali masing-masing koefisien sehingga menghasilkan nilai 30

 3 → 30 :  3 = x10
10 → 30 : 10 =  x3

Kemudian, lakukan eliminasi dengan menggunakan nilai masing-masing pengali

2x + 3y = 17.000   |x10 
x + 10y = 34.000 _ | x3

Diperoleh:

20x + 30y = 170.000
 3x + 30y = 102.000 _
17x       =  68.000

 17x      =  68.000 
 17            17

x = 4.000

Diperoleh, harga sebuah buku adalah Rp 4.000,-

#2 Langkah Substitusi

Karena harga buku telah diketahui melalui solusi variabel x = 4000, selanjutnya dihitung harga pulpen dengan metode substitusi

x = 4.000
Pulpen direpresentasikan oleh variabel y
Sehingga substitusi nilai x ke salah satu persamaan soal untuk mencari solusi numerik y

   2x + 3y = 17.000
⇔ 2(4.000) + 3y = 17.000
⇔ 3y = 17.000 - 8.000
⇔ 3y = 9.000

⇔  3y  =  9.000 
    3        3
⇔ y = 3.000

Diperoleh, harga sebuah pulpen adalah Rp 3.000,-

Jawaban: Harga buku adalah Rp 4.000,- dan harga pulpen adalah Rp 3.000,-

Baca juga: Daftar Isi Pelajaran Matematika

---

Sekian artikel "SPLDV dan Contoh Soalnya". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih ...