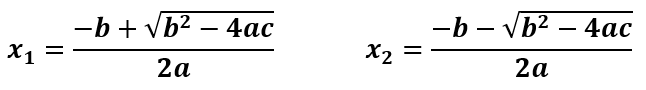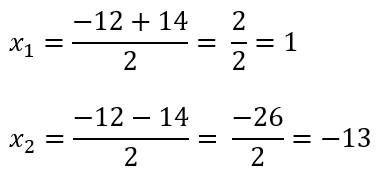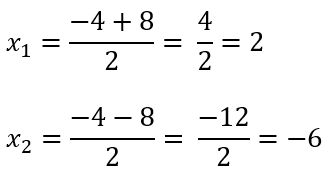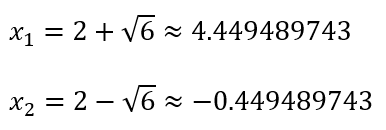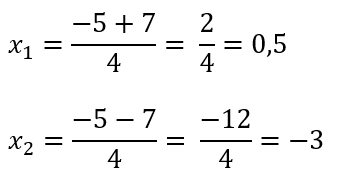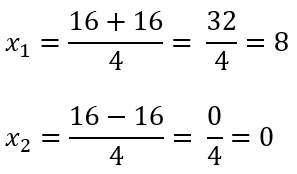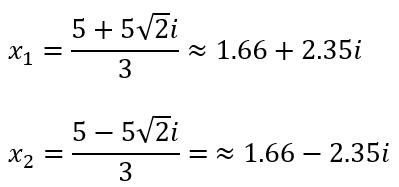A. Materi Rumus ABC dan Solusi Akar Persamaan Kuadrat
Rumus ABC adalah rumus alternatif untuk mencari solusi akar-akar persamaan kuadrat menggunakan nilai a, b, dan c berdasarkan konsep penyempurnaan bentuk kuadrat. Metode ini juga disebut dengan "Quadratic Formula". Nilai b dan c tidak harus ada dalam persamaan kuadrat yang dihitung, karena nilai tersebut dapat diganti dengan nol dalam rumus ABC.
Sehingga diperoleh solusi akar-akar untuk x1 dan x2 sebagai berikut.
Rumus ABC mempunyai kelebihan untuk menghitung persamaan kuadrat dengan solusi irasional dan kompleks. Namun, rumus ini akan menjadi rumit saat dibandingkan dengan metode faktorisasi untuk persamaan kuadrat dengan solusi bulat dan rasional. Sebagai alternatif, penggunaan bantuan kalkulator saat menggunakan rumus ABC dapat mempercepat perhitungannya.
Navigasi Cepat
B. Konsep Perumusan Rumus ABC (Quadratic Formula)
Perumusan rumus ABC secara aljabar berasal dari metode melengkapi kuadrat sempurna atau "completing the square". Berikut proses aljabar dari solusi akar-akar yang dihasilkan metode melengkapi kuadrat sempurna ke dalam bentuk rumus ABC.
B1. Konsep Melengkapi Kuadrat Sempurna
Metode melengkapi kuadrat sempurna merupakan pendekatan geometri untuk menghitung akar-akar persamaan kuadrat. Berikut formulasi metode melengkapi kuadrat sempurna untuk menghitung solusi akar persamaan kuadrat.
Baca juga: Materi Melengkapi kuadrat Sempurna dan Contoh Soal
B1. Proses Aljabar Solusi Akar ke Rumus ABC
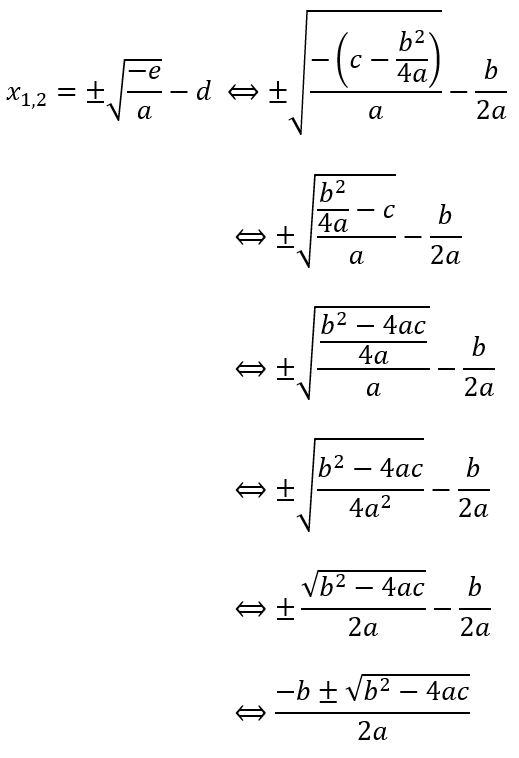
Proses ini mengubah rumus akar-akar yang dihasilkan metode melengkapi kuadrat sempurna; menggunakan nilai a, b, dan c dalam bentuk umum persamaan kuadrat. Hal ini melatarbelakangi nama rumus ABC sebagai rumus praktis, karena dapat digunakan langsung terhadap bentuk umum persamaan kuadrat.
Sehingga diperoleh solusi akar-akar untuk x1 dan x2 sebagai berikut.
C. Contoh Soal Persamaan Kuadrat Menggunakan Rumus ABC
Berikut beberapa contoh soal mencari akar-akar persamaan kuadrat menggunakan rumus ABC.
Contoh 1. Hitung Solusi Akar Persamaan Kuadrat x²+12x-13=0 dengan Rumus ABC!
Penyelesaian:
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari x²+12x-13=0 adalah x1 = 1 dan x2 = -13.
Contoh 2. Hitung Solusi Akar Persamaan Kuadrat x²+4x-12=0 dengan Rumus ABC!
Penyelesaian:
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari x²+4x-12=0 adalah x1 = 2 dan x2 = -6.
Contoh 3. Hitung Solusi Akar Persamaan Kuadrat x²-4x-2=0 dengan Rumus ABC!
Penyelesaian:
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari x²-4x-2=0 adalah x1 ≈ 4.449489743 dan x2 ≈ -0.449489743.
Contoh 4. Hitung Solusi Akar Persamaan Kuadrat 2x²+5x-3=0 dengan Rumus ABC!
Penyelesaian:
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari 2x²+5x-3=0 adalah x1 ≈ 0,5 dan x2 ≈ -3.
Contoh 5. Hitung Solusi Akar Persamaan Kuadrat 2x²-16x=0 dengan Rumus ABC!
Penyelesaian:
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari 2x²-16x=0 adalah x1 ≈ 8 dan x2 ≈ 0.
Contoh 6. Hitung Solusi Akar Persamaan Kuadrat 3x²-10x+25=0 dengan Rumus ABC!
Penyelesaian:
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari 3x²-10x+25=0 adalah x1 ≈ 1,66 + 2,35i dan x2 ≈ 1,66 -2,35i.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Rumus ABC | Alternatif Mencari Akar Persamaan Kuadrat dan Contoh Soal". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...