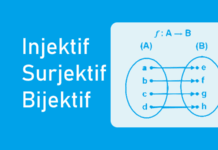
A. Definisi dan Notasi Fungsi
Sebagaimana di materi dasar fungsi, definisi fungsi adalah istilah relasi khusus dalam ilmu matematika yang memetakan tepat satu-satu elemen himpunan daerah asal (domain) ke elemen himpunan daerah kawan (kodomain). Fungsi dalam konteks relasi dinotasikan sebagai f : A → B. Berikut akan dijelaskan mengenai nilai fungsi, notasi, domain, kodomain, range, dan grafik fungsi dalam koordinat kartesius.
Navigasi Cepat
- A. Definisi dan Notasi Fungsi
- B. Daerah Asal (Domain) Fungsi
- C. Daerah Kawan (Kodomain) Fungsi
- D. Daerah Hasil (Range) Fungsi
A1. Notasi Fungsi dan Contohnya
Notasi fungsi dalam konteks secara umum dinotasikan dengan huruf kecil misalnya f(x), g(x), h(x), dan lainnya. Misalnya notasi relasi fungsi f : A → B dapat diubah ke bentuk notasi fungsi umum.
f : A → B f(A) = B B = f(A)
Penggambaran fungsi umumnya digambarkan dalam koordinat kartesius. Berikut dasar notasi fungsi sebagai fungsi yang memetakan sumbu x (domain) ke sumbu y (kodomain) dalam koordinat kartesius di R².
f : x → y f(x) → y y = f(x)
Misalnya diketahui bentuk beberapa persamaan fungsi berikut.
y = 2x + 3 y = 4x + 8 y = 3x - 7 Ketiga fungsi di atas dapat dinotasikan dalam notasi fungsi f(x) = 2x + 3 g(x) = 4x + 8 h(x) = 3x - 7
A2. Nilai Fungsi dan Contohnya
Nilai fungsi adalah nilai yang yang dihasilkan oleh substitusi suatu elemen domain ke dalam fungsinya. Semua nilai fungsi menghasilkan himpunan daerah hasil yang disebut range.
Suatu fungsi f(x) = 2x + 1, tentukan nilai fungsi untuk x = 2 dan x = 3 terhadap fungsi f(x)!
Penyelesaian:
Nilai fungsi f(x) untuk x = 2
Dapat diketahui model fungsi f(x) adalah 2x + 1
f(x) = 2x + 1
f(2) = 2(2) + 1
= 4 + 1
= 5
Nilai fungsi f(x) untuk x = 3
f(x) = 2x + 1
f(3) = 2(3) + 1
= 6 + 1
= 7
Jadi, nilai fungsi f(2) = 5 dan f(3) = 7.
B. Daerah Asal (Domain)
Daerah asal (domain) suatu fungsi adalah himpunan elemen-elemen yang dimasukkan ke dalam model suatu fungsi. Dalam diagram relasi fungsi, domain merupakan himpunan pertama yang berelasi.
Contoh:
1. Suatu fungsi f(x) = 2x mempunyai domain bilangan bulat x < 10 dan x > 0, tulis notasi domain fungsi f(x) dan elemen-elemennya!
Df = {0 < x < 10 | x bilangan bulat}
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
2. Suatu fungsi g(x) = 3x + 3 mempunyai domain bilangan real x ≥ 0, tulis notasi domain fungsi f(x) dan elemen-elemennya!
Dg = {x ≥ 0 | x bilangan real}
= {0, 0.00..., ..., 1, 1.00..., ..., ∞}
Banyak bilangan real antara 2 bilangan bulat adalah tidak terhingga, sulit untuk menuliskannya secara langsung.
C. Daerah Kawan (Kodomain)
Daerah kawan suatu fungsi adalah himpunan yang memuat nilai-nilai fungsi yang mungkin. Himpunan kodomain dapat memuat elemen-elemen lain yang tidak termasuk dalam nilai fungsinya. Namun, semua nilai fungsinya (range) harus ada dalam kodomain fungsinya.
Contoh C1: Soal Kodomain Fungsi
Suatu fungsi f(x) = 1, dapat mempunyai kodomain berupa bilangan bulat {1, 2, 3}, karena dapat diketahui range fungsinya adalah {1}
D. Range Fungsi
Range suatu fungsi adalah himpunan daerah hasil yang merupakan himpunan semua nilai fungsi, hasil dari substitusi tiap elemen-elemen domain terhadap model fungsinya.
Contoh D1: Menentukan range fungsi diskrit dan grafiknya
Hitung range fungsi f(x) = x + 1 dengan himpunan domain x = {1, 2, 3, 4} dan plot grafik fungsi tersebut dalam koordinat kartesius!
Penyelesaian:
f(x) = x + 1
Df = {1, 2, 3, 4}
# Menghitung Range Fungsi
Menghitung range fungsi dilakukan dengan membuat tabel substitusi elemen x ke model fungsi f(x)
f(x) = x + 1
f(1) = 1 + 1 = 2 f(2) = 2 + 1 = 3 f(3) = 3 + 1 = 4 f(4) = 4 + 1 = 5
Sehingga diperoleh tabel berikut.
| x | 1 | 2 | 3 | 4 |
| f(x) | 2 | 3 | 4 | 5 |
Jadi, range fungsi f(x) adalah {2, 3, 4, 5}.
# Membuat Grafik Fungsi
Elemen fungsi f(x) merupakan nilai diskrit (titik-titik nilai) yaitu domain {1, 2, 3, 4} dengan range {2, 3, 4, 5}. Sehingga grafik fungsi yang dihasilkan berupa titik-titik range dalam koordinat kartesius.
Berikut grafik yang dihasilkan tabel di langkah sebelumnya.
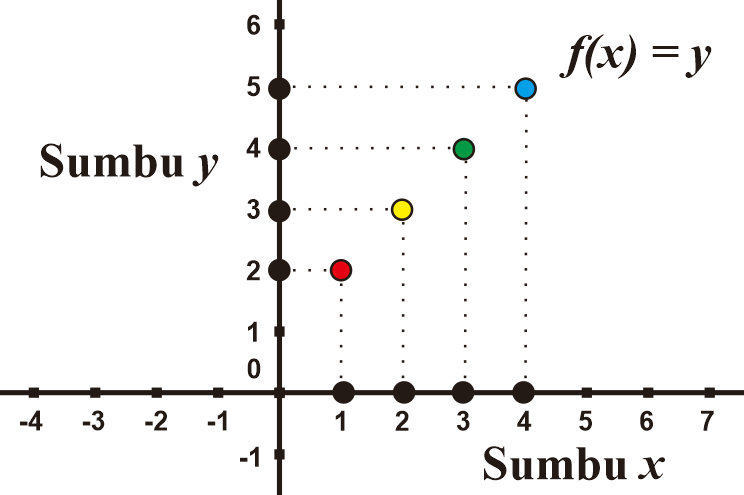
Contoh D2: Menentukan range fungsi interval dan grafiknya
Hitung range fungsi g(x) = x² dengan himpunan domain x dengan -3 ≤ x ≤ 3 | x ∈ ℝ, dan plot grafik fungsi tersebut dalam koordinat kartesius!
Penyelesaian:
g(x) = x²
Dg = {-3 ≤ x ≤ 3 | x ∈ ℝ}
Sehingga, domain fungsi g(x) merupakan interval bilangan real dari -3 hingga 3.
# Menghitung Range Fungsi
Menghitung range fungsi dilakukan dengan membuat tabel substitusi elemen x ke model fungsi f(x). Domain fungsi merupakan interval bilangan real, sehingga range fungsi yang dihasilkan juga termasuk interval bilangan real.
Untuk mempermudah perhitungan dapat dilakukan pengujian titik-titiknya dalam interval tertentu, misalnya interval 0.5 dari {-3 ≤ x ≤ 3 | x ∈ ℝ} diperoleh -3, -2.5, -2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2, 2.5 3.
g(x) = x²
g(-3) = (-3)² = 9 g(-2.5) = (-2.5)² = 6.25 g(-2) = (-2)² = 4 g(-1.5) = (-1.5)² = 2.25 g(-1) = (-1)¹ = 1 g(-0.5) = (-0.5)² = 0.25 g(0) = (0)² = 0 g(0.5) = (0.5)² = 0.25 g(1) = (1)² = 1 g(1.5) = (1.5)² = 2.25 g(2) = (2)² = 4 g(2.5) = (2.5)² = 6.25 g(3) = (3)² = 9
Sehingga diperoleh tabel berikut.
| x | -3 | -2.5 | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| g(x) | 9 | 6.25 | 4 | 2.25 | 1 | 0.25 | 0 | 0.25 | 1 | 2.25 | 4 | 6.25 | 9 |
Jadi, range fungsi g(x) adalah {0 ≤ Rg ≤ 9 | Rg ∈ ℝ}.
# Membuat Grafik Fungsi
Elemen fungsi g(x) merupakan interval bilangan real, yaitu domain {-3 ≤ x ≤ 3 | x ∈ ℝ} dengan range {0 ≤ Rg ≤ 9 | Rg ∈ ℝ}. Sehingga grafik fungsi g(x) dapat menghasilkan garis dalam koordinat kartesius.
Berikut grafik yang dihasilkan tabel di langkah sebelumnya.
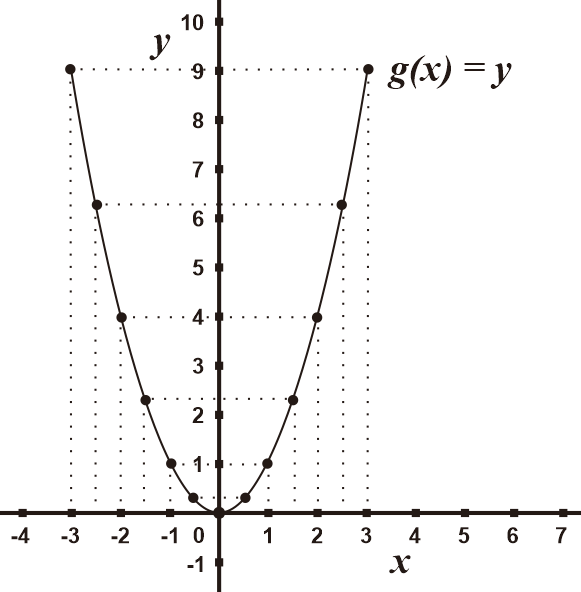
Sehingga grafik yang dihasilkan fungsi g(x) dengan domain {-3 ≤ x ≤ 3 | x ∈ ℝ} adalah garis kurva.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Notasi Fungsi, Daerah Asal (Domain), Daerah Kawan (Kodomain), dan Range". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...