A. Pengertian Fungsi Linear dan Bentuk Umum
Fungsi linear adalah fungsi yang disusun oleh persamaan aljabar yaitu berupa konstanta maupun suku berderajat satu, sehingga menghasilkan garis linear dalam koordinat kartesius. Garis linear merupakan istilah matematika untuk garis lurus. Sebagaimana dalam konsep aljabar, konstanta merupakan suatu nilai tetap, misalnya: 1, 2, Π (3.14...), dan e (angka Euler). Sedangkan suku berderajat satu merupakan bentuk ekspresi aljabar dengan nilai pangkat variabel sama dengan satu.
Navigasi Cepat
A1. Bentuk Umum Fungsi Linear
Berikut bentuk umum fungsi linear
f : x → ax + b atau dalam notasi fungsi umum f(x) = ax + b y = ax + b atau dengan menggunakan definisi kemiringan garis (gradien), koefisien a dapat diganti menjadi koefisien gradien m f(x) = mx + b y = mx + b
dengan
a = koefisien variabel x
Nilai a dalam bentuk umum fungsi linear f(x) = ax + b merepresentasikan kemiringan garis (gradien) dalam koordinat kartesius, sehingga bentuk umum f(x) = ax + b dapat ditulis menjadi f(x) = mx + b.
b = merupakan suatu nilai tetap (konstanta)
Nilai b dalam bentuk umum fungsi f(x) = ax + b merepresentasikan titik potong garis terhadap sumbu y di koordinat kartesius.
A2. Contoh Fungsi Linear
Berikut beberapa contoh fungsi linear
- f(x) = 2x + 1 (bentuk umum)
- y = -4x + 2 (bentuk umum)
- f(x) = x (bentuk umum)
- f(x) = 3 (bentuk umum)
- y = 5 (bentuk umum)
- x = x + 1 (bentuk umum)
- 3y = 3x + 1 (bukan bentuk umum)
- 2y = -x + 5 (bukan bentuk umum)
Pada contoh di atas, fungsi 3y = 3x + 1 dan 2y = -x +1 merupakan fungsi linear walaupun tidak mematuhi bentuk umum fungsi linear. Kedua fungsi tersebut diubah ke bentuk umumnya dengan menjadikan koefisien y menjadi 1.
Contoh mengubah ke bentuk umum fungsi linear
Mengubah 3y = 3x + 1 ke bentuk umum fungsi linear
3y = 3x + 1 ⇔ y = x + 1/3 atau f(x) = x + 1/3 Jadi, bentuk umumnya adalah f(x) = x + 1/3
Mengubah 2y = -x + 5 ke bentuk umum fungsi linear
2y = -x + 5 ⇔ y = -1/2x + 5/2 atau f(x) = -1/2x + 5/2 Jadi, bentuk umumnya adalah f(x) = -1/2x + 5/2
B. Grafik Fungsi Linear dan Contohnya
B1. Cara Membuat Grafik Fungsi Linear
Berikut beberapa langkah untuk membuat grafik fungsi linear dalam koordinat kartesius
- Mengidentifikasi fungsi linear
- Apakah fungsi termasuk linear?
- Apakah fungsi sudah sesuai dengan bentuk umum fungsi linear?
- Jika belum, ubah persamaan ke bentuk umum fungsi linear
- Merancang grafik fungsi linear
- Apakah fungsi mempunyai konstanta c?
- Jika tidak, maka c = 0 dan grafik fungsi memotong titik pusat koordinat kartesius di (0, 0)
- Jika ya, maka fungsi memotong sumbu y dengan nilai c
- Apakah fungsi mempunyai variabel bebas (ax)?
- Lakukan substitusi ke model fungsi minimal 2 nilai bebas
- Apakah fungsi mempunyai konstanta c?
- Menggambar Grafik
- Menandai titik rancangan grafik
- Titik Potong
- Dan titik hasil substitusi
- Menarik garis dari titik-titik yang telah ditandai
- Menandai titik rancangan grafik
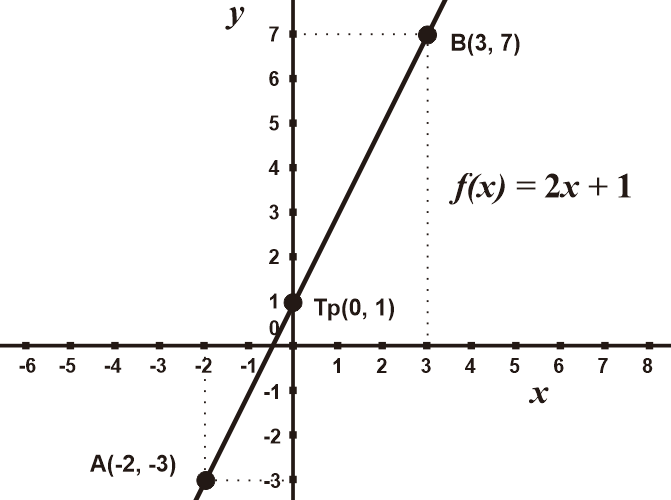
Contoh 1: Grafik Fungsi f(x) = 2x + 1
# Identifikasi fungsi linear f(x) = 2x + 1
Fungsi termasuk linear, karena terdiri dari konstanta dan suku berderajat satu
Fungsi sudah sesuai dengan bentuk umum fungsi linear
# Perancangan grafik f(x) = 2x + 1
Mempunyai nilai c = 1, sehingga titip potong sumbu y di titik Tp(0, 1)
Mempunyai koefisien a = 2, sehingga m > 0 dan grafik miring ke kanan
Substitusi nilai acak misalnya diambil nilai acak -2 dan 3 diperoleh
f(x) = 2x + 1
y = 2x + 1
f(-2) = 2(-2) + 1
= -3
Diperoleh titik A(x, y) = A(-2, -3)
f(2) = 2(3) + 1
= 7
Diperoleh titik B(x, y) = B(3, 7)
# Menggambar grafik f(x) = 2x + 1
Sehingga dapat dibuat grafik berikut dalam koordinat kartesius
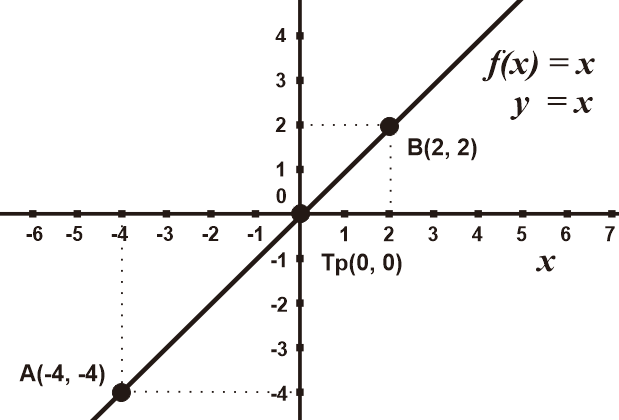
Contoh 2: Grafik Fungsi y = x
# Identifikasi fungsi y = x
Fungsi termasuk linear, karena tersusun dari suku berpangkat 1
Fungsi sudah sesuai dengan bentuk umum fungsi linear y = x ⇔ f(x) = x
# Perancangan grafik fungsi y = x
Tidak mempunyai nilai c atau c = 0, sehingga grafik memotong titik koordinat Tp(0, 0)
Mempunyai koefisien a = 1, sehingga m > 0 dan grafik miring ke kanan
Substitusi nilai acak misalnya diambil nilai acak -4 dan 2 diperoleh
y = x
⇔ f(x) = x
f(-4) = x
= -4
Diperoleh titik A(x, y) = (-4, -4)
f(2) = x
= 2
Diperoleh titik B(x, y) = (2, 2)
# Menggambar fungsi y = x
Sehingga dapat dibuat grafik berikut dalam koordinat kartesius
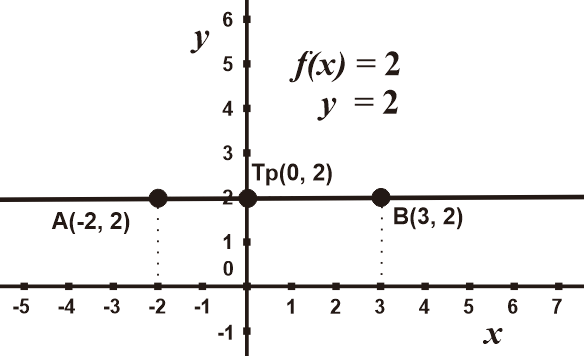
Contoh 3: Grafik Fungsi y = 2
#Identifikasi fungsi y = 2
Fungsi termasuk linear karena tersusun dari konstanta
Fungsi sudah sesuai dengan bentuk umum fungsi linear y = 2 ⇔ f(x) = 2
# Perancangan grafik fungsi y = 2
Fungsi mempunyai nilai c = 2, sehingga grafik memotong sumbu y di Tp(0, 2)
Fungsi tidak mempunyai variabel bebas, sehingga nilai a = 0 dan grafik berbentuk horizontal
Substitusi nilai acak misalnya diambil nilai acak -2 dan 3 diperoleh
y = 2 ⇔ f(x) = 2 f(-2) = 2 Diperoleh titik A(-2, 2) f(3) = 2 Diperoleh titik B(3, 2) ∴ Dapat diketahui semua nilai yang disubstitusikan akan bernilai 2
# Menggambar fungsi y = 2
Sehingga dapat dibuat grafik berikut dalam koordinat kartesius
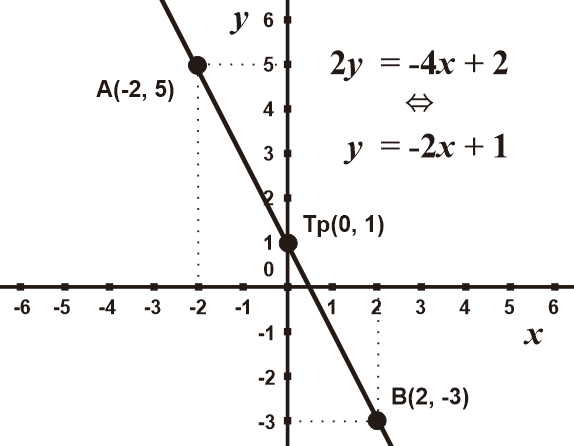
Contoh 4: Grafik Fungsi 2y = -4x + 2
# Identifikasi fungsi 2y = -4x + 2
Fungsi merupakan linear karena tersusun oleh konstanta dan suku berderajat satu
Fungsi belum memenuhi bentuk umum fungsi linear, karena ruas kanan untuk variabel y mempunyai koefisien bukan satu
Sehingga untuk merancang grafik, fungsi diubah ke dalam bentuk umum fungsi linear
2y = -4x + 2
⇔ y = -4x + 2
2
⇔ y = -2x + 1
f(x) = -2x + 1
Sehingga bentuk umum fungsi linear dari 2y = -4x + 2 adalah f(x) = -2x + 1
# Perancangan grafik fungsi dalam bentuk umumnya f(x) = -2x + 1
Bentuk umum mempunyai nilai c = 1, sehingga grafik fungsi memotong sumbu y di Tp(0, 1)
Bentuk umum mempunyai koefisien a = -2, sehingga m < 0 dan grafik miring ke kiri
Substitusi nilai bebas, misalnya -2 dan 2 diperoleh
2y = -4x + 2
⇔ y = -2x + 1
f(x) = -2x + 1
f(-2) = -2(-2) + 1
= 4 + 1
= 5
Diperoleh titik A(-2, 5)
f(2) = -2(2) + 1
= -4 + 1
= -3
Diperoleh titik B(2, -3)
# Menggambar grafik fungsi dalam bentuk umumnya
Sehingga diperoleh gambar grafik berikut
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Fungsi Linear | Pengertian Fungsi Linear, Grafik, dan Contoh Soal". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...


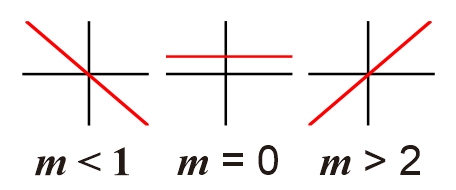








Paling lengkap grafik fungsi linear.
Terima kasih atas ulasannya Kak Muhammad Arif 🙂