A. Pengertian Segitiga dan Rumus Segitiga
Segitiga adalah bangun datar yang terdiri dari 3 sisi garis lurus dengan 3 titik sudut yang berjumlah 180º. Sejak tahun 300 SM, Euclid menemukan konsep bahwa jumlah ketiga sudut segitiga adalah 180º. Hal ini memberikan kontribusi yang besar dalam konsep bangun datar, seperti mencari panjang sisi dan panjang sudut.
Artikel terkait: Rumus Volume Limas Segitiga dan Luas Permukaan
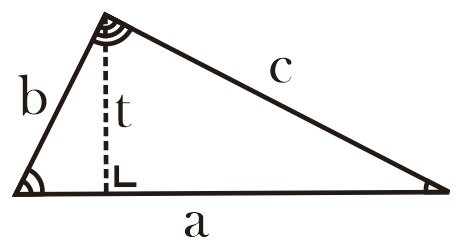
Keterangan:
a = alas
t = tinggi, tinggi segitiga membentuk sudut 90° terhadap alasnya.
b, c = sisi lain segitiga
B. Rumus Segitiga
| Nama | Rumus |
|---|---|
| Luas (L) | L = ½ × a × t |
| Keliling (Kll) | Kll = a + b + c |
| Tinggi (t) | t = (2 × Luas) ÷ a |
| Alas (a) | a = (2 × Luas) ÷ t |
1. Contoh Soal Mencari Luas dan Keliling Segitiga
Diketahui suatu segitiga dengan panjang sisi alas a = 4 cm, sisi b = 3 cm, sisi c = 5 cm dan t = 3 cm. Hitunglah keliling dan luas segitiga tersebut!
Diketahui:
a = 4 cm, b = 3 cm, c = 5 cm, t = 3 cm
Ditanya:
Keliling dan luas!
Penyelesaian:
Keliling = a + b + c
Keliling = 4 cm + 3 cm + 5 cm
Keliling = 12 cm
Luas = ½ × a × t
Luas = ½ × 4 cm × 3 cm
Luas = 6 cm²
Jadi, keliling segitiga adalah 12 cm dan luas segitiga 6 cm².
2. Contoh Soal Mencari Tinggi Segitiga
Diketahui suatu segitiga mempunyai luas 18 cm² dan sisi alas 4 cm. Tentukan tinggi segitiga!
Diketahui:
Luas = 18 cm², a = 4 cm
Ditanya:
Tinggi segitiga!
Penyelesaian:
Tinggi = (2 × Luas) ÷ a
Tinggi = (2 x 18 cm²) ÷ 4 cm
Tinggi = 36 cm² ÷ 4 cm = 9 cm
Jadi, tinggi segitiga adalah 9 cm.
3. Contoh Soal Mencari Alas Segitiga
Diketahui suatu segitiga mempunyai luas 16 cm² dan tinggi 8 cm. Tentukan alas segitiga!
Diketahui:
Luas = 16 cm², a = 8 cm
Ditanya:
Alas segitiga!
Penyelesaian:
Alas = (2 × Luas) ÷ t
Alas = (2 x 16 cm²) ÷ 8 cm
Alas = 32 cm² ÷ 8 cm = 4 cm
Jadi, alas segitiga adalah 4 cm.
C. Jenis-jenis Segitiga
Jenis-jenis segitiga secara umum dapat diketahui dari panjang sisi dan besar sudutnya,
1. Jenis Segitiga Berdasarkan Panjang Sisi
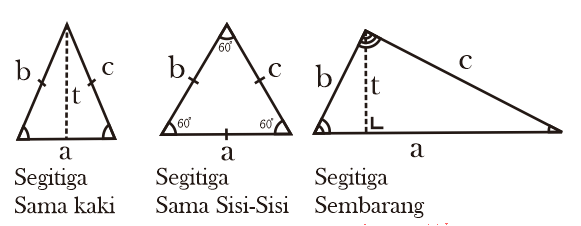
Berdasarkan Panjang sisinya segitiga dapat dibedakan menjadi 3 yaitu segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang.
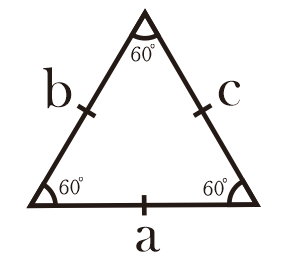
1.a. Segitiga Sama Sisi (Equilateral Triangle)
Segitiga sama sisi adalah segitiga yang ketiga sisinya mempunyai panjang sama yang menyebabkan ketiga sudutnya mempunyai ukuran 60º.
Artikel terkait: Rumus Segitiga Sama Sisi
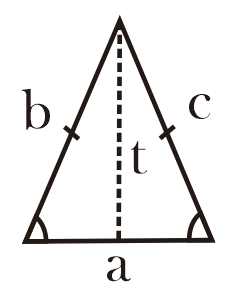
1.b. Segitiga Sama Kaki (Isosceles Triangle)
Segitiga sama kaki adalah segitiga yang mempunyai 2 sisi sama panjang yang menyebabkan 2 sudutnya memiliki besar yang sama.
1.c. Segitiga Sembarang (scalene triangle)
Segitiga sembarang adalah segitiga dengan ketiga panjang sisinya berbeda-beda, sehingga ketiga besar sudutnya juga berbeda-beda.
2. Jenis Segitiga Berdasarkan Besar Sudutnya
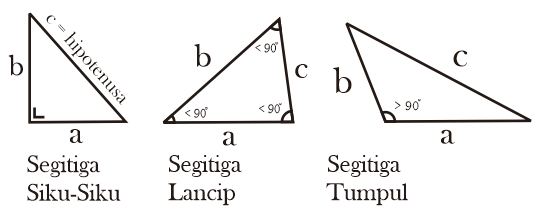
Berdasarkan besar sudutnya segitiga dapat dibedakan menjadi 3 yaitu segitiga siku-siku, segitiga lancip, dan segitiga tumpul.
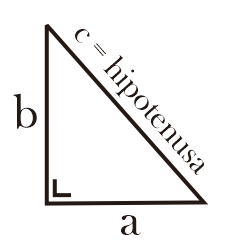
2.a. Segitiga Siku-Siku (Right Triangle)
Segitiga siku-siku adalah segitiga yang salah satu sudutnya membentuk sudut siku-siku (90º). Pada segitiga siku-siku, 2 sisinya akan membentuk sudut 90º. Sisi yang tidak membentuk sudut siku-siku disebut sisi miring (hipotenusa).
Artikel terkait: Rumus Pythagoras Segitiga Siku-Siku
2.b. Segitiga Lancip (Acute Triangle)
Segitiga lancip adalah segitiga yang masing-masing sudut besarnya kurang dari 90°.
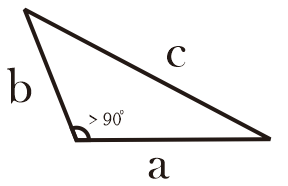
2.c. Segitiga Tumpul (Obtuse Triangle)
Segitiga tumpul adalah segitiga yang salah satu besar sudutnya lebih dari 90°.
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel Rumus Segitiga | Jenis Segitiga, Rumus Luas dan Keliling Segitiga. Nantikan artikel menarik lainnya dan mohon share dan juga menyukai Fans Page Advernesia. Terima kasih…


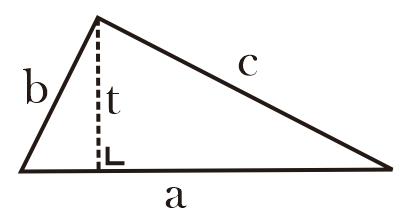
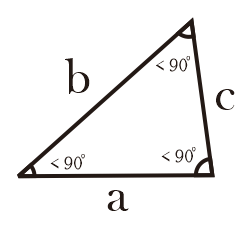













bangun-bangun yang ada diatas adalah macam-macam bangung datar.rumus dan cara penyelesaian setiap bangun berbeda
Hai kak Mimik Winarti, benar sekali cara penyelesaian bangun datar memang berbeda, sesuai dengan bentuknya, adapun untuk kasus yang rumit dapat menggunakan Kalkulus Lanjut untuk melakukan estimasi.
mudah dimengerti sekali ka aaa lup lup deh♡
Terima kasih Ileano Dirgantara atas ulasannya
Senang dapat membantu 🙂
Singkat, padat, dan mudah dimengerti. 👍
Terima kasih atas reviewnya kak Nia dari situs Penjaga Perpus 🙂
Halo kak,
Gimana cari rumus sisi C nya..
Jika diketahui segitiga siku- siku alas 6cm tinggi 2cm berapa panjang sisi C.?..
Mohon penjelasan.
Rumus luas dari segitiga sembarang dan segitiga lancip apa mimik?
Hai, I Gusti Ayu Puspitasari
Secara sederhana semua bangun segitiga mempunyai rumus umum pada tabel di atas
Untuk eksplorasi lebih lanjut dapat memanfaatkan konsep dasar lainnya, misalnya sudut, trigonometri, dan lain-lain
Semoga membantu 🙂
Alhamdulillah rumus rumus ini sangat lengkap