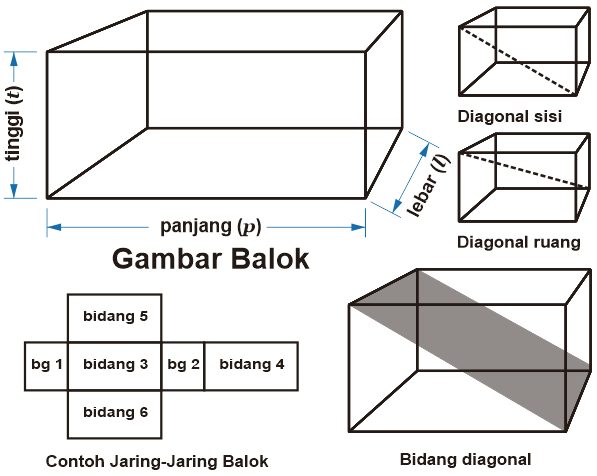
A. Pengertian Balok atau Cuboid
Balok adalah bangun ruang tiga dimensi yang tersusun oleh 3 pasang segi empat (persegi atau persegi panjang) dan paling sedikit mempunyai 1 pasangan sisi segi empat yang mempunyai bentuk yang berbeda. Sebelum mempelajari rumus volume balok dan luas permukaan balok, sebaiknya kita memahami sifat-sifat balok, bagian-bagian balok, dan jaring-jaring balok.
Artikel terkait: Rumus Kubus | Volume Kubus dan Luas Permukaan Kubus
B. Sifat-Sifat Balok, Bagian Balok, dan Jaring-Jaring Balok
Berikut sifat-sifat umum balok:
- Balok tersusun dari 3 pasang sisi yang sama (total 6 buah sisi).
- Setiap sisi berbentuk segiempat yaitu persegi atau persegi panjang.
- Paling sedikit harus mempunyai 1 pasang sisi dengan bentuk yang berbeda.
- Mempunyai 12 rusuk.
- Rusuk-rusuk yang sejajar mempunyai ukuran yang sama.
- Mempunyai 4 diagonal bidang.
- Diagonal bidang yang sejajar mempunyai ukuran yang sama.
- Mempunyai 4 diagonal ruang dan semuanya mempunyai ukuran yang sama.
- Setiap bidang diagonal berbentuk persegi panjang.
C. Rumus Balok
t = tinggi, p = panjang, l = lebar
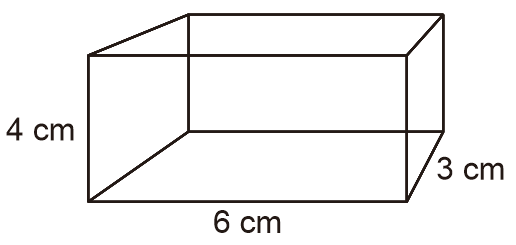
Contoh 1: Menghitung Volume dan Luas Permukaan Balok
Hitunglah volume dan luas permukaan balok berikut!
Diketahui:
p = 6 cm
l = 3 cm
t = 4 cm
Ditanya:
Volume (V) dan Luas Permukaan (L) Balok
Penyelesaian:
V = p × l × t
V = 6 cm × 3 cm × 4 cm
V = 72 cm³
L = 2 × (p.l + p.t +l.t)
L = 2 × ((6 cm × 3 cm) + (6 cm × 4 cm) + (3 cm × 4 cm))
L = 2 × (18 cm² + 24 cm² + 12²)
L = 2 × 54 cm²
L = 108 cm²
Jadi, volume balok adalah 72 cm³ dan luas permukaan balok adalah 108 cm².
Contoh 2: Cara Menghitung Panjang Balok Jika Diketahui Luas Permukaannya
Sebuah balok mempunyai luas permukaan 52 cm², jika diketahui lebar balok 2 cm dan tinggi balok 3 cm. Hitunglah panjang balok tersebut!
Diketahui:
L = 52 cm²
l = 2 cm
t = 3 cm
Ditanya:
Panjang balok (p)
Penyelesaian:
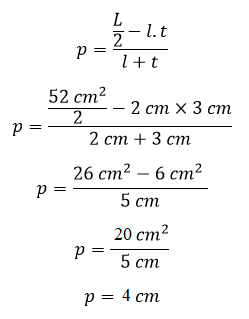
Jadi, panjang balok adalah 4 cm.
Contoh 3: Cara Menghitung Panjang Balok Jika Diketahui Volume
Sebuah balok mempunyai volume 12 cm³, jika diketahui lebar balok 2 cm dan tinggi balok 2 cm. Hitunglah panjang balok tersebut!
Diketahui:
V = 12 cm³
l = 2 cm
t = 2 cm
Ditanya:
Panjang balok (p)
Penyelesaian:
p = V ÷ l ÷ t
p = 12 cm³ ÷ 2 cm ÷ 2 cm
p = 3 cm
Jadi, panjang balok adalah 3 cm.
Contoh 4: Cara Menghitung Lebar Balok Jika Diketahui Luas Permukaannya
Sebuah balok mempunyai luas permukaan 214 cm², jika diketahui panjang balok 7 cm dan tinggi balok 5 cm. Hitunglah lebar balok tersebut!
Diketahui:
L = 214 cm²
p = 7 cm
t = 5 cm
Ditanya:
Lebar balok (l)
Penyelesaian:
Jadi, lebar balok adalah 6 cm.
Contoh 5: Cara Menghitung Lebar Balok Jika Diketahui Volume
Sebuah balok mempunyai volume 336 cm³, jika diketahui panjang balok 8 cm dan tinggi balok 6 cm. Hitunglah lebar balok tersebut!
Diketahui:
V = 336 cm³
p = 8 cm
t = 6 cm
Ditanya:
Lebar balok (l)
Penyelesaian:
l = V ÷ p ÷ t
l = 336 cm³ ÷ 8 cm ÷ 6 cm
l = 7 cm
Jadi, panjang lebar adalah 7 cm.
Contoh 6: Cara Menghitung Tinggi Balok Jika Diketahui Luas Permukaannya
Sebuah balok mempunyai luas permukaan 382 cm², jika diketahui panjang balok 9 cm dan lebar balok 8 cm. Hitunglah tinggi balok tersebut!
Diketahui:
L = 382 cm²
p = 9 cm
l = 8 cm
Ditanya:
Tinggi balok (l)
Penyelesaian:
Jadi, tinggi balok adalah 7 cm.
Contoh 7: Cara Menghitung Tinggi Balok Jika Diketahui Volume
Sebuah balok mempunyai volume 7120 cm³, jika diketahui panjang balok 10 cm dan lebar balok 8 cm. Hitunglah tinggi balok tersebut!
Diketahui:
V = 720 cm³
p = 10 cm
l = 8 cm
Ditanya:
Tinggi balok (l)
Penyelesaian:
l = V ÷ p ÷ l
l = 720 cm³ ÷ 10 cm ÷ 8 cm
l = 9 cm
Jadi, panjang lebar adalah 9 cm.
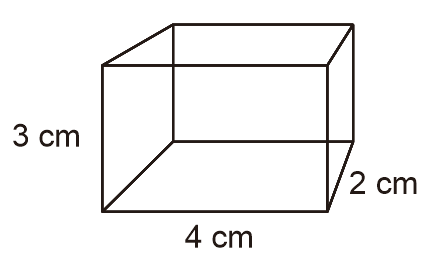
Contoh 8: Menghitung Diagonal Bidang, Diagonal Ruang, dan Luas Bidang Diagonal
Hitunglah panjang diagonal bidang, diagonal ruang, dan luas bidang diagonal balok di bawah!
Diketahui:
p = 4 cm
l = 2 cm
t = 3 cm
Penyelesaian:
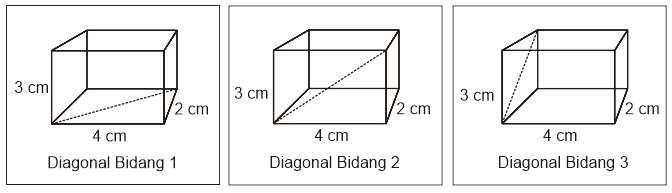
Panjang diagonal bidang
Balok mempunyai 12 diagonal bidang dan dibagi menjadi 3 kelompok diagonal bidang
Dengan panjang masing-masing, dapat dihitung menggunakan rumus Pythagoras
Artikel terkait: Rumus Pythagoras Segitiga dan Contoh Soalnya
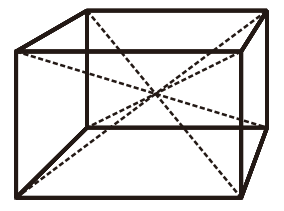
Panjang diagonal ruang
Balok mempunyai 4 diagonal ruang yang sama panjang
Dengan panjang setiap diagonal ruang
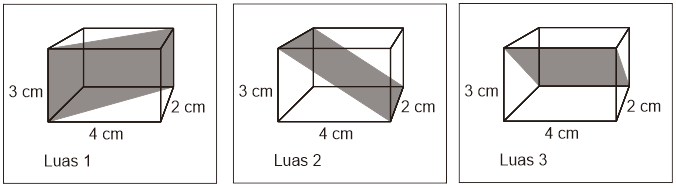
Luas bidang diagonal
Balok mempunyai 3 pasangan luas bidang diagonal (total 6 bidang diagonal):
Dengan luas setiap bidang diagonal
Kontributor: Bambs (Pemeriksa)
Animasi Balok: Pierce, Rod - Math is Fun
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Rumus Volume Balok dan Rumus Luas Permukaan Balok”. Nantikan artikel menarik lainnya dan mohon untuk share dan juga menyukai Fans Page Advernesia. Terima kasih…

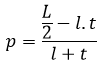
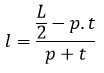
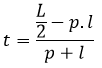
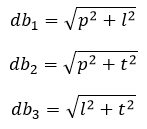
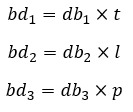
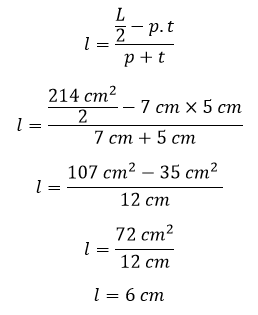
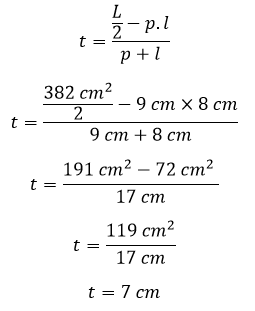
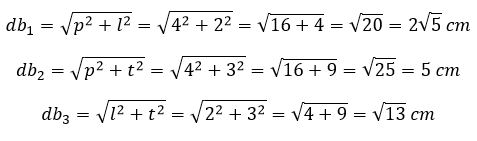
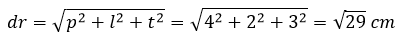




Sangat berguna, terimakasih 🤗
Terima kasih kembali Yunie atas reviewnya ya 🙂
Kak kalau mau mencari tinggi dari sebuah balok yang diketahui volume sama luas alasnya saja bagaimana?
Contohnya: volume: 1500 dm
Luas alas : 125 dm
?
Kak kalau mau mencari tinggi dari sebuah balok yang diketahui volume sama luas alasnya saja bagaimana?
Contohnya: volume: 1500 dm
Luas alas : 125 dm
Ringkas dan Jelas sangat bermanfaat. Terimakasih 👍
Terima kasih Kak Ratnasari
Senang dapat membantu 🙂
sangat bermanfaat...singkat,jelas,padat👍
Terima kasih Kak Delarsa atas ulasannya
Senang dapat membantu 🙂
Senang bisa belajar matematika bersama kakak.apakah kakak mempunyai akun brainly ?
Hai, Yasir
Senang dapat membantu Yasir dalam belajar matematika
Sayangnya Kakak tidak mempunyai akun Brainly
Namun, tenang saja kok, Yasir dapat mengajukan pertanyaan dan melihat artikel Matematika lainnya di bagian Daftar Isi
Begitu juga artikel di Advernesia terus ditambah untuk materi-materi lainnya 🙂
bagaimana mencari panjang, lebar dan tinggi suatu balok jika yang diketahui hanyalah volume