Dalam konsep dasar bilangan dikenal istilah faktor dan kelipatan. Pemahaman kedua istilah ini penting diketahui untuk mempelajari materi selanjutnya seperti FPB dan KPK hingga mencari solusi dari suatu persamaan matematika. Berikut dijelaskan mengenai faktor, faktor persekutuan, kelipatan, kelipatan persekutuan, KPK dan FPB.
Navigasi Cepat
A. Faktor Bilangan, Faktor Persekutuan, dan FPB
Sebelum menghitung FPB, perlu diketahui cara menghitung faktor bilangan dan faktor persekutuan dari dua atau lebih bilangan.
A.1 Faktor Bilangan
Faktor bilangan adalah satu atau lebih bilangan lain yang habis membagi bilangan tersebut.
Contoh 1: Faktor dari 6
Penyelesaian
Karena 6 habis dibagi 1, 2, 3, 6; yaitu
6 : 1 = 6
6 : 2 = 3
6 : 3 = 2
6 : 6 = 1
Baca juga: Cara Pembagian Bersusun
Tidak ada bilangan selain 1, 2, 3, 6 yang habis membagi 6. Dari pembagian tersebut, warna pembagi yang digaris bawahi akan menjadi pasangan dalam tabel faktor, karena hasil perkalian masing-masing pasangan adalah 6. Jadi, dapat dibentuk tabel faktor berikut.
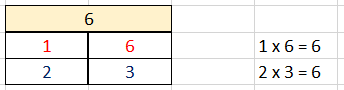
Jadi, faktor dari bilangan 6 adalah 1, 2, 3, dan 6
Baca juga: Cara Menghitung Perkalian
Contoh 2: Faktor dari 12
Penyelesaian
Karena 12 habis dibagi 1, 2, 3, 4, 6, 12; yaitu
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 1 = 12
Dengan mengikuti langkah contoh sebelumnya, dapat dibuat tabel faktor dari 12.
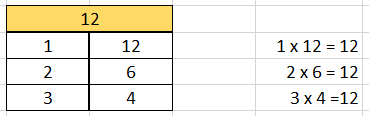
Jadi, faktor dari bilangan 12 adalah 1, 2, 3, 4, 6, dan 12
A.2 Faktor Persekutuan
Faktor persekutuan adalah faktor yang sama dari dua bilangan atau lebih.
Contoh: Faktor persekutuan dari 18 dan 32
Penyelesaian
Untuk mencari nilai faktor persekutuan, dihitung terlebih dahulu masing-masing faktor dari 18 dan 32.
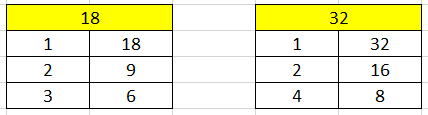
Sehingga dari tabel diketahui
Faktor dari 18 adalah 1, 2, 3, 6, 9, dan 18.
Faktor dari 32 adalah 1, 2, 4, 8, 16, dan 32.
Faktor persekutuan merupakan nilai faktor yang sama di kedua faktor bilangan 18 dan 32 yaitu 1 dan 2.
Jadi, faktor persekutuan dari 18 dan 32 adalah 1 dan 2
A.3 Faktor Persekutuan Besar (FPB)
Faktor persekutuan besar (FPB) adalah nilai faktor persekutuan terbesar dari dua bilangan atau lebih.
Untuk mencari FPB dapat dilakukan dengan konsep dasar atau dengan cara yang lebih cepat menggunakan pohon faktor (disediakan di bawah).
Contoh 1: FPB dari 24 dan 32 (Konsep Dasar)
Penyelesaian:
Untuk mencari FPB, dicari terlebih dahulu faktor dari 24 dan 32 sebagai berikut
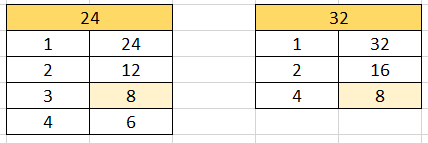
Faktor masing-masing bilangan
Faktor 24 adalah 1, 2, 3, 4, 6, 8, 12, dan 24
Faktor 32 adalah 1, 2, 4, 8, 16, dan 32
Kemudian dihitung faktor persekutuan kedua bilangan adalah
Faktor persekutuan 24 dan 32 adalah 1, 2, 4, dan 8
FPB merupakan nilai faktor persekutuan terbesar yaitu 8
Jadi, FPB dari 24 dan 32 adalah 8
Mencari FPB dengan Pohon Faktor (Cara Cepat)
FPB dari 63 84 dan 126 adalah ...
Penyelesaian
Tips: Cara mencari faktor prima suatu bilangan menggunakan pohon faktor adalah dengan membagi bilangan secara terus menerus dengan bilangan prima terkecil yang mungkin.
Baca juga: Cara Mencari Faktorisasi dengan Bilangan Prima
Cara mencari FPB dengan pohon faktor adalah dengan mengalikan bilangan yang sama pada faktorisasi pohon faktor dari masing-masing bilangan dengan menggunakan pangkat terkecil.
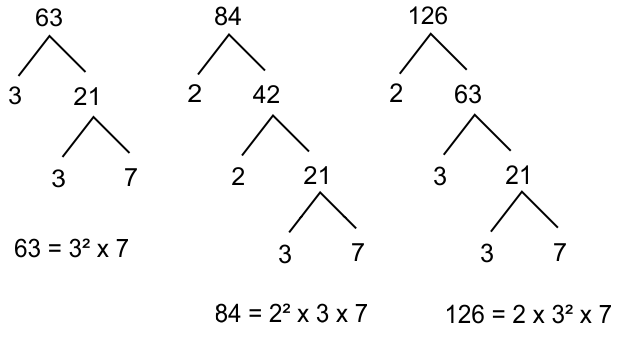
Sehingga diperoleh hasil faktorisasi prima masing-masing bilangan
63 = 3² × 7
84 = 2² × 3 × 7
126 = 2 × 3² × 7
Kalikan bilangan yang sama pada faktorisasi prima dengan menggunakan pangkat terkecil.
Bilangan yang sama dari faktorisasi prima 63, 84, 126 adalah 3 (pangkat terkecil 1) dan 7 (pangkat terkecil 1)
FPB = 3 × 7 = 21
Jadi, FPB dari 63, 84, dan 126 adalah 21
B. Kelipatan, Kelipatan Persekutuan, dan KPK
Sebelum menghitung KPK, perlu diketahui konsep kelipatan dan kelipatan persekutuan.
B.1 Kelipatan
Kelipatan adalah hasil dari menambahkan bilangan dengan dirinya sendiri secara berurut atau mengalikan bilangan secara terurut.
Contoh: Kelipatan 3
Penyelesaian
Ini diperoleh dengan cara,
(3+3), (3+3+3), (3+3+3+3), dan seterusnya
atau
(1×3), (2×3), (3×3), (4×3), dan seterusnya
Jadi, kelipatan 3 adalah 3, 6, 9, 12 dan seterusnya.
B.2 Kelipatan Persekutuan
Kelipatan persekutuan adalah kelipatan yang sama dari dua bilangan atau lebih.
Contoh: Kelipatan persekutuan dari 6 dan 8
Penyelesaian
Untuk mencari kelipatan persekutuan, terlebih dahulu dihitung kelipatan masing-masing bilangan
Kelipatan 6 adalah 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, dan seterusnya.
Kelipatan 8 adalah 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, dan seterusnya.
Dari hasil perhitungan dapat diketahui nilai kelipatan yang sama adalah 24 dan 48, namun masih terdapat banyak nilai kelipatan persekutuan yang belum terhitung.
Jadi, kelipatan persekutuan 6 dan 8 adalah 24, 48, dan seterusnya.
B.3 Kelipatan Persekutuan Kecil (KPK)
Kelipatan persekutuan kecil (KPK) adalah nilai kelipatan persekutuan terkecil dari dua atau lebih bilangan.
Contoh 1: KPK dari 20 dan 40
Penyelesaian
Sebelum menghitung KPK, perlu dihitung kelipatan masing-masing bilangan
Kelipatan 20 adalah 20, 40, 60, 80, dan seterusnya
Kelipatan 40 adalah 40, 80, 120, 160, dan seterusnya
Dari perhitungan di atas diketahui kelipatan persekutuannya 40, 80, dan seterusnya. Karena mencari KPK maka hasilnya adalah nilai kelipatan persekutuan terkecil yaitu 40.
Jadi, KPK dari 20 dan 40 adalah 40.
Mencari KPK dengan Pohon Faktor (Cara Cepat)
KPK dari 12 15 dan 45 adalah ...
Tips: Cara mencari faktor prima suatu bilangan menggunakan pohon faktor adalah dengan membagi bilangan secara terus menerus dengan bilangan prima terkecil yang mungkin.
Baca juga: Cara Mencari Faktorisasi dengan Bilangan Prima
Cara mencari KPK dengan pohon faktor adalah dengan mengalikan semua bilangan faktorisasi pada pohon faktor dari masing-masing bilangan dengan menggunakan pangkat terbesar.
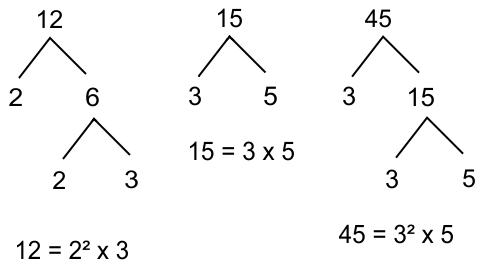
Sehingga diperoleh hasil faktorisasi prima masing-masing bilangan
12 = 2² × 3
15 = 3 × 5
45 = 3² × 5
dilanjutkan dengan mengalikan semua bilangan hasil faktorisasi prima dengan menggunakan pangkat terbesar
KPK = 2² × 3² × 5 = 4 × 9 × 5 = 180
Jadi, KPK dari 12, 15, dan 45 adalah 180
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “FPB dan KPK | Faktor & Kelipatan Persekutuan | Faktor dan Kelipatan”. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…














👍👍👍👍👍👍👍
Terima kasih, Eska Febrina Syari 🙂
Terimakasih sangat jelas dan sangat membantu
Terima kasih Azzam atas review-nya
Senang dapat membantu 🙂
Terima kasih sudah membuat artikel ini, cukup membantu juga bagi para orang tua murid yang mau belajar lagi pelajaran ini. Apalagi kalau dulu waktu sekolah belum mengerti mengenai FPB dan KPK, artikel ini cukup membantu bagi para orang tua untuk mengerti sehingga bisa membantu anaknya dalam pembelajaran matematika khususnya mengenai FPB dan KPK
Hai, kak Hanto
Senang dapat membantu anak kakak
Terima kasih banyak atas ulasannya 🙂
Mau Tanya sebenarnya pelajaran sekolah INI mau dilanjutkan seperti sediakala atau selesai ,(game over).
Anak anak jadi malas belajar Dan ga mau melihat buku. Jadi pengennya main gadget terus!!
Mohon kebijakannya Dari Lara guru!
Terimakasih
Hai, Kak Eridwiagus
Melihat kondisi pandemi ini, tidak apa main gadget kak,
Asalkan hal yang diakses itu mendukung untuk pendidikannya di sekolah kak ...
Tentunya itu ada campur tangan orang tua untuk mengontrol penggunaan gadget anak kakak
Sehingga terhindar dari hal-hal yang tidak layak untuk anak kakak
Semoga membantu 🙂
Terimakasih, sangat membantu
Terima kasih kembali atas ulasannya Kak Aga
Senang dapat membantu 🙂
Terima kasha sangat sangat membantu