A. Pengertian Aljabar atau Algebra
Aljabar adalah bagian dari ilmu matematika meliputi teori bilangan, geometri, dan analisis penyelesaiannya. Secara harfiah, aljabar berasal dari bahasa arab yaitu الجبر atau yang dibaca "al-jabr". Ilmu ini dibuat oleh Muḥammad ibn Mūsā al-Khwārizmī dalam bukunya mengenai konsep dan bentuk aljabar ditulis sekitar tahun 820, yang merupakan seorang matematikawan, astronomer, dan geograf. Ia dijuluki sebagai "The Father of Algebra". Dalam bahasa inggris, aljabar dikenal dengan istilah "algebra".
Navigasi Cepat:
- Rumus Persamaan
- Variabel (Peubah)
- Koefisien (Coefficient)
- Konstanta (Constant)
- Eksponen (Pangkat)
- Derajat
- Suku
B. Bentuk Aljabar dan Rumus Aljabar Dasar
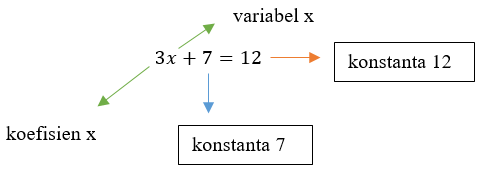
Bentuk aljabar adalah teknik yang digunakan untuk menyajikan suatu masalah matematika dengan simbol atau huruf sebagai peubah suatu objek dalam masalah tersebut. Terdapat 7 istilah umum yang perlu diketahui untuk memahami bentuk suatu aljabar dasar, yaitu:
-
Rumus Persamaan
Persamaan adalah suatu teknik matematika yang digunakan untuk menyamakan suatu permasalahan ke bentuk matematika dengan tanda persamaan atau sama dengan (=). Bentuk ini dapat berupa bentuk yang paling sederhana hingga kompleks. Persamaan dapat digunakan untuk membentuk suatu rumus matematika terhadap suatu masalah.
Contoh:
Masalah: Jumlah kelereng Xeon dan Yuni adalah 10 buah. Jika kelereng yuni sebanyak 3 buah, berapa jumlah kelereng Xeon? Diketahui: Ubah Kelereng Yuni menjadi variabel y Ubah kelereng Xeon menjadi variabel x y = 3, maka nilai y adalah 3 x + y = 10 Catatan: x + y = 10 merupakan persamaan matematika dari jumlah kelereng Xeon dan Yuni Ditanya: berapakah nilai x? Penyelesaian: x + y = 10 x = 10 - y Pada dasarnya untuk memindahkan suatu nilai ke ruas lain, sama artinya dengan menghilangkan nilai tersebut di ruas asal. Berikut penjelasannya untuk kasus di atas. x + y = 10 x + y - y = 10 - y x = 10 - y Sehingga, untuk mempercepat perhitungan dapat langsung menulis lawan nilai yang dipindahkan. x + y = 10 x = 10 - y Diketahui nilai y = 3, diperoleh x = 10 - 3 = 7 Karena nilai x = 7 Jadi, kelereng Xeon berjumlah 7 buah -
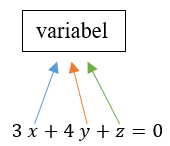
Variabel (Peubah)
Variabel adalah suatu simbol atau huruf yang digunakan untuk menggantikan suatu nilai yang bersifat tidak tetap (berubah-ubah tergantung persamaan yang memuatnya). Variabel dalam bahasa inggris disebut dengan "variable" (dieja ˈve(ə)rēəbəl) , dan juga disebut "peubah" dalam bahasa Indonesia. Variabel dapat disimbolkan dengan huruf latin (a, A, b, B, c, D, dst).
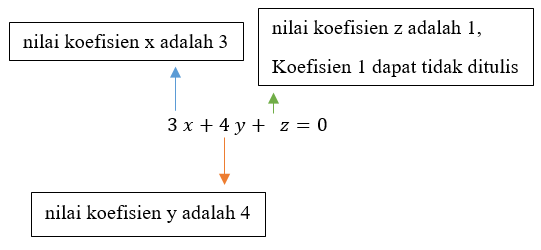
Pada persamaan tersebut, terdapat 3 variabel yaitu x, y, dan z.
-
Koefisien (Coefficient)
Koefisien adalah nilai yang digunakan untuk mengalikan suatu variabel. Koefisien dalam bahasa inggris disebut dengan "coefficient". Nilai koefisien = 1 dapat tidak ditulis.
3.1 Menghitung variabel dengan koefisien
Suatu persamaan 3x = 12, berapakah nilai variabel x? Penyelesaian: 3x = 12 3 * x = 12 x = 12/3 = 4 Catatan: perpindahan koefisien suatu ruas = membagi ruas lain dengan nilai koefisien tersebut Jadi, variabel x = 4
3.2 Menghitung variabel dengan koefisien pada persamaan
Menghitung nilai koefisien menjadi lebih kompleks saat ia berada pada suatu persamaan
Untuk menyelesaikan solusi variabel x dapat diperoleh dengan memisahkan semua objek selain x keruas kanan, berikut:
Untuk menyelesaikan solusi variabel y dapat diperoleh dengan memisahkan semua objek selain y keruas kanan, berikut:
-
Konstanta (Constant)
Konstanta adalah suatu nilai yang bersifat tetap (constant) pada suatu bentuk aljabar. Konstanta dalam bahasa inggris disebut dengan "constant". Ciri-ciri yang paling umum suatu konstanta yaitu tidak berikatan dengan suatu variabel. Untuk rumus-rumus khusus, konstanta dapat disimbolkan dengan huruf (misalnya: a, b, lainnya) atau berupa simbol khusus.
4.1 Contoh konstanta pada persamaan umum
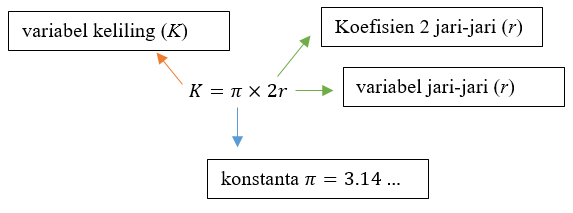
4.2 Contoh konstanta pada rumus khusus
Suatu konstanta pada rumus-rumus khusus disimbolkan dengan nilai tertentu, misalnya rumus keliling lingkaran:
-
Eksponen (Pangkat)
Suatu variabel dalam suatu bentuk aljabar dapat memuat pangkat (eksponen). Operasi pangkat mempunyai prioritas kedua sejajar dengan operasi akar setelah tanda kurung dalam operasi hitung matematika.
Misalnya nilai x adalah 4, maka dapat dihitung nilai y sebagai berikut:
Baca juga: Cara Menghitung Perpangkatan Bilangan dan Sifatnya
-
Derajat
Derajat pada suatu bentuk aljabar adalah nilai pangkat tertinggi yang dimuat variabel bentuk aljabar, berikut contohnya:
Bentuk Aljabar Derajat 3x 1 3x2 + 1 2 3x2 + 2x + 1 2 4x4 + 2y2 + 1 4 5x6 + y 6 -
Suku
Suku pada bentuk aljabar adalah total elemen yang dimuat oleh suatu bentuk aljabar. Suku digunakan untuk mempermudah mengkomunikasikan bentuk aljabar sehingga mudah untuk dibahasakan, berikut contohnya:
Aljabar s1 s2 s3 s4 suku 2x 2x - - - 1 2x+1 2x 1 - - 2 3x2+2x-1 3x2 2x 1 - 3 4x3+3x2+2x-1 4x3 3x2 2x 1 4 dan lainnya ... ... ... ... ... Suku-suku bentuk aljabar dibedakan menjadi suku sejenis dan suku tak sejenis:
7.1 Suku Sejenis
Suku sejenis adalah suku-suku yang mempunyai variabel dengan pangkat yang sama.
a) x, 2x, 3x, 4x, dan lain-lain.
b) xy3, 2xy3, 8xy3, dan lain-lain.
7.2 Suku Tak Sejenis
Suku tidak sejenis adalah suku-suku yang tidak mempunyai variabel yang sama.
a) 2x, 2y, 3z, 4w, dan lain-lain.
b) 8xy3, 3xy, dan lain-lain.
C. Operasi Aljabar
Operasi aljabar pada umumnya hampir sama dengan operasi hitung bilangan bulat.
Baca juga: Operasi Hitung Bilangan dan Urutannya
C1. Operasi Penjumlahan dan Pengurangan Aljabar
Operasi penjumlahan dan pengurangan aljabar hanya dapat dilakukan pada suku-suku sejenis.
Contoh 1: Menyederhanakan aljabar
Sederhanakan bentuk aljabar 2x + 3y + 7x - 2y?
Penyelesaian:
# urutkan suku-suku yang sejenis 2x + 3y + 7x - 2y = 2x + 7x + 3y - 2y = (2x + 7x) + (3y - 2y) = 9x + y
Jadi, bentuk sederhana dari 2x + 3y + 7x - 2y adalah 9x + y
C2. Operasi Perkalian Aljabar
Contoh 1: Perkalian dengan konstanta
Perkalian dengan konstanta dilakukan dengan mengalikan nilai koefisien masing-masing variabel yang dioperasikan.
-
2y × 3 = 6y
-
(3y + x) × 4 = (3y × 4) + (x × 4) = 12y + 4x
-
3yz × 7 = 21yz
Contoh 2: Perkalian dengan variabel
perkalian dengan variabel dilakukan secara menyeluruh, baik koefisien maupun variabelnya.
-
y × y = y2
-
x2 × x = x2 + 1 = x3
-
2yz × y = 2y2z
-
(2x + 1) y = (2x × y) + (1 × y) = 2xy + y
C3. Operasi Pembagian Aljabar
Untuk mempermudah operasi pembagian aljabar, dilakukan dengan cara mengubah ke bentuk pecahan.
Contoh 1: Pembagian variabel dengan konstanta
Contoh 2: Pembagian variabel dengan variabel
Contoh 3: Pembagian variabel dengan variabel yang lebih kompleks
C4. Operasi Perpangkatan Aljabar
Contoh 1:
Kontributor: Luthfifahreza (Pemeriksa) dan Rere Prasasti (Pemeriksa)
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Aljabar | Bentuk Aljabar, Rumus Aljabar, dan Operasi Aljabar“. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih ...


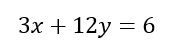
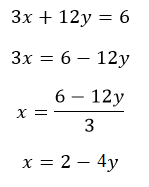
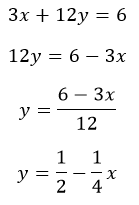

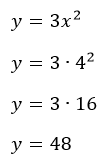
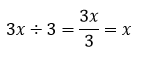
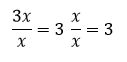
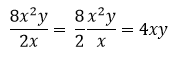










9p x 8q x 7r x 2p
8a x (-5b) x 2c
5 x a x b
P x p x p x p x p x p
Tentukan koefisien dari x, y, z pada bentuk aljabar berikut
A. 3x + 8my - 2z
B. 5ax + 10by +3z
Debutkan suku² sejenis bentuk aljabar berikut
A. 9x² + 8y + 5y + 8
B. 8x² - 5x + 7x² + 8x - 3
C. 6x³ - 5x² + 7x - 2x³ + 6x - 7
Dalam menentukan faktor sekutunya, faktorkan bentuk aljabar berikut
a. 10a-5
b. 15p²q²+3pq
Hasil operasi aljabar berikut
(2x-3)-(x-5)
Ini gimana ya ka
|-49|-|-45|+ |23|
rumusnya gmn kak ?
terima kasih atas sharingnya kak, sangat bermanfaat
Terima kasih Dik Aisyah Hasibuan atas ulasannya
Senang dapat membantu proses belajarnya 🙂
blog paling bermanfaat dan penjelasannya sangat mudah di pahami. terima kasih kak atas ilmu yang kakak bagikan. semoga sukses selalu
Enak kak penyampainnya
Jdi lebih gampang paham ^^
Makasi kak
sederhanakanlah 2p. 2q . 2r menggunakan rumus a pangkat m x a pangkat n= a pangkat m+n
(2y+4)÷6y + 3×4 -5y=....?
Kalau (-4a+3b) (3a²+2a -5) gmn rumusnya?
Bisa menggunakan teknik perluasan kurung Kak Jevika
Semoga membantu