A. Sistem Koordinat Kartesius (Koordinat Titik)
A1. Pengertian Koordinat Kartesius
Sistem koordinat kartesius adalah sistem identifikasi titik dalam bidang menggunakan serangkaian bilangan dengan menggunakan garis-garis sumbu (axes) tegak lurus sebagai pengukurnya. Sehingga sistem koordinat kartesius juga disebut sistem koordinat titik. Koordinat kartesius ditemukan pada abad ke-17 oleh matematikawan Perancis yang bernama René Descartes. Ia merevolusi ilmu matematika dengan menyediakan hubungan antara geometri Euclidean dan aljabar. Sistem koordinat kartesius dalam bahasa inggris disebut dengan "cartesian coordinate system".
Baca juga: Pengertian Titik, Garis, Bidang, dan Ruang
A2. Sistem Koordinat Kartesius
Konsep sistem koordinat kartesius menggunakan garis sumbu yang berupa garis-garis tegak lurus untuk mengidentifikasi posisi titik dalam suatu bidang. Jumlah garis sumbu mengikuti konsep geometri Euclidean di dimensi-n. Koordinat kartesius 2 dimensi mempunyai 2 garis sumbu (x, y). Begitu pula sistem koordinat 3 dimensi mempunyai 3 garis sumbu (x, y, z). Artikel ini membahas lebih lanjut mengenai dasar sistem koordinat kartesius di dimensi 2.
A3. Koordinat Kartesius Dimensi 2
Koordinat kartesius di dimensi 2 mempunyai 2 garis sumbu yang saling tegak lurus, yaitu sumbu x dan sumbu y. Berikut ilustrasi sistem koordinat kartesius 2 dimensi.
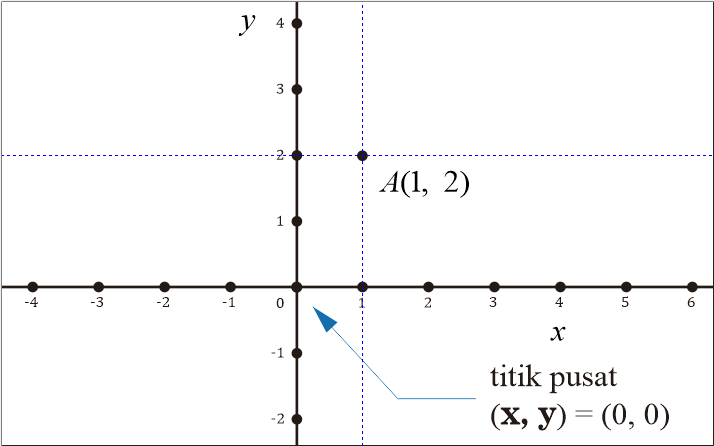
Koordinat kartesius di dimensi 2 mempunyai dua sumbu yaitu sumbu x dan y, sebagai berikut.
- Sumbu x adalah garis identifikasi titik yang berbentuk horizontal dalam koordinat kartesius. Pengukuran dengan sumbu x suatu titik disebut dengan absis.
- Sumbu y adalah garis identifikasi titik yang berbentuk vertikal dalam koordinat kartesius. Pengukuran dengan sumbu y suatu titik disebut dengan ordinat.
- Titik pusat koordinat kartesius adalah titik potong tiap sumbu dalam koordinat kartesius. Titik ini digunakan sebagai titik acuan setiap sumbu untuk mengukur posisi suatu titik.
- Identifikasi titik-titik dalam koordinat kartesius menggunakan rangkaian (x, y). Misalnya titik A di atas mempunyai koordinat (x, y) = (1, 2). Ini berarti titik a mempunyai posisi 1 di sumbu x dan posisi 2 di sumbu y. Sehingga dapat ditulis A(1, 2) atau A saja dalam koordinat kartesius dua dimensi.
Baca juga: Pengertian Garis Vertikal dan Horizontal
A4. Pembagian Kuadran Koordinat Kartesius 2 Dimensi
Pembagian daerah pada koordinat kartesius 2-D disebut dengan kuadran (quadrant) yang terdiri dari 4 daerah. Pembagian daerah ini digunakan dalam konsep matematika lainnya, misalnya sudut dan trigonometri. Penamaan kuadran dilakukan secara memutar berlawanan arah jarum jam.
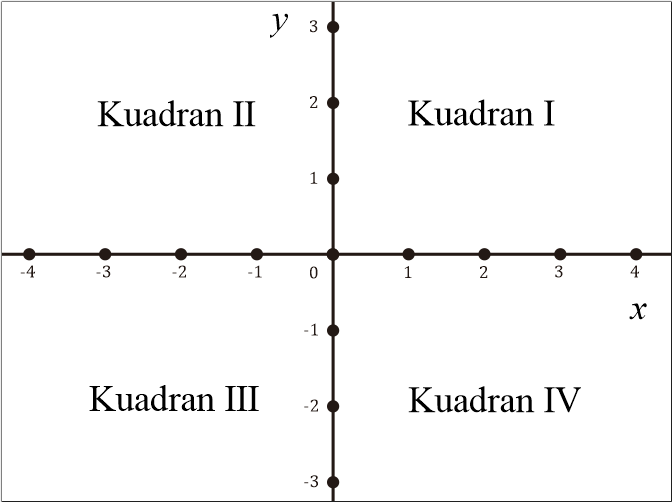
Berikut pembagian daerah kuadran pada koordinat kartesius.
-
Kuadran I
Kuadran I koordinat kartesius adalah daerah yang dimuat oleh sumbu x positif (+) dan sumbu y positif (+).
-
Kuadran II
Kuadran II koordinat kartesius adalah daerah yang dimuat oleh sumbu x negatif (-) dan sumbu y positif (+).
-
Kuadran III
Kuadran III koordinat kartesius adalah daerah yang dimuat oleh sumbu x negatif (-) dan sumbu y negatif (-).
-
Kuadran IV
Kuadran IV koordinat kartesius adalah daerah yang dimuat oleh sumbu x positif (+) dan sumbu y negatif (-).
-
Titik Koordinat dan titik yang berimpit dengan garis sumbu
Titik koordinat dan titik yang berimpit dengan garis sumbu tidak termasuk dalam daerah kuadran, yang ditandai dengan adanya nilai 0 pada aksis atau ordinatnya.
Contoh: (0, 0); (0, 2); dan (-1, 0)
B. Contoh Soal Identifikasi Titik Koordinat
Perhatikan titik-titik dalam koordinat kartesius berikut.
Cari masing-masing koordinat titik A, B, C, D dan daerah kuadrannya!
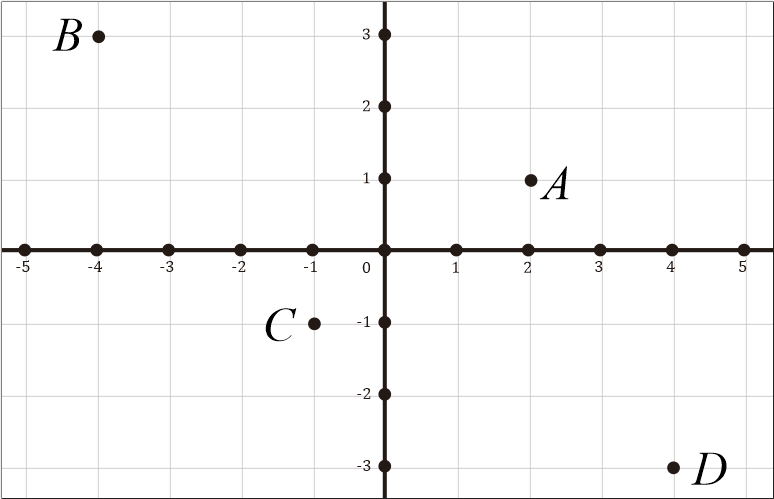
Penyelesaian:
Dari gambar dapat diamati posisi titik A, B, C, D; sehingga diperoleh hasil berikut.
| Titik | x (absis) | y (ordinat) | Koordinat | Kuadran |
| A | 2 | 1 | A(2, 1) | I |
| B | -4 | 3 | B(-4, 3) | II |
| C | -1 | -1 | C(-1, -1) | III |
| D | 4 | -3 | D(4, 3) | IV |
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Koordinat Kartesius | Pengertian, Sistem, Kuadran, dan Titik Koordinat". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...











