Pengertian Perbandingan atau Ratios
Perbandingan adalah ukuran yang digunakan untuk membandingkan suatu nilai terhadap nilai lainnya dengan satuan sejenis. Setiap nilai yang dibandingkan harus mempunyai satuan yang sama, misalnya satuan panjang, berat, dan waktu. Dalam bahasa inggris, perbandingan juga disebut dengan "ratios". Berdasarkan konsep matematika, rumus perbandingan dapat ditulis dalam bentuk pecahan (fraction), tanda colon (:), atau ditulis biasa. Misalnya, "1 banding 2" dapat ditulis "1 : 2".
Contoh Kasus Perbandingan:
- Perbandingan tinggi badan 2 orang anak; satuan panjang.
- Perbandingan berat komputer dan berat laptop; satuan berat.
- Perbandingan nilai ulangan 3 orang siswa; satuan nilai ulangan.
Navigasi Cepat
- A. Rumus Perbandingan
- B. Menyederhanakan Perbandingan
- C. Cara Menghitung Nilai Perbandingan
- D. Jenis-Jenis Perbandingan
A. Rumus Perbandingan
Rumus perbandingan menggunakan konsep dasar pembagian. Cara menghitung perbandingan hampir sama dengan membentuk kasus yang dibandingkan ke bentuk pecahan.
Artikel terkait: Materi Pecahan dan Jenisnya
Syarat membentuk rumus perbandingan
- Satuan harus sejenis, misalnya panjang, berat dan waktu.
- Bentuk satuan harus sama, misalnya cm, kg, menit.
Contoh 1: Membandingkan Umur
- Umur Ahmad 10 tahun
- Umur Made 30 tahun
Berapakah perbandingan umur Ahmad dan Made?
Penyelesaian:
Satuan = tahun
Ahmad : Made = 10 : 30
Jadi, perbandingan umur Ahmad dan Made adalah 10 : 30
FPB 10 dan 30 adalah 10
Artikel terkait: Cara Menghitung FPB dan KPK
Perbandingan 10 : 30 dapat disederhanakan menjadi 1 : 3
Jadi, perbandingan umur Ahmad dan Made juga dapat ditulis sebagai 1 : 3
Contoh 2: Membandingkan Berat
- Berat Andi 1 kwintal
- Berat Beni 45 kg
- Berat Kristi 10.000 gram
Berapakah perbandingan berat Andi, Beni dan Kristi?
Penyelesaian:
Sebelum diubah ke bentuk perbandingan perlu disamakan jenis satuan berat ketiga orang tersebut
- Andi 1 kwintal = 100 kg
- Beni 45 kg
- Kristi 10.000 gram = 10 kg
Andi : Beni : Kristi = 100 : 45 : 10
FPB 100, 45 dan 10 adalah 5
Dapat disederhanakan menjadi
Andi : Beni : Kristi = 100/5 : 45/5 : 10/5
Andi : Beni : Kristi = 20 : 9 : 2
Jadi, perbandingan berat Andi, Beni, dan Kristi adalah 20 : 9 : 2
B. Cara Menyederhanakan Perbandingan
Untuk menyederhanakan bentuk suatu perbandingan, sama halnya seperti menyederhanakan pecahan yaitu menggunakan FPB.
Contoh: Menyederhanakan Perbandingan Umur
Perbandingan umur Ahmad dan Made 10 : 30
Berdasarkan konsep pecahan dapat ditulis
#Menyederhanakan dengan FPB
Faktor 10 adalah 1, 2, 5, 10
Faktor 30 adalah 1, 2, 3, 10, 15, 30
FPB 10 dan 30
Artikel terkait: 4 Cara Menyederhanakan Pecahan
Jadi, bentuk sederhana perbandingan 10 : 30 adalah 1 : 3
C. Cara Menghitung Perbandingan
Dalam penerapannya, perbandingan digunakan sebagai bahasa di lingkungan sehari-hari. Perbandingan sama artinya dengan menjadikan satu.
Rumus Menghitung Hasil Perbandingan
Contoh: Menghitung Hasil Perbandingan
Seorang pengusaha yang ingin bergerak di bisnis produksi makanan mendapatkan modal dari seorang investor untuk membentuk suatu perusahaan. Pengusaha dan investor setuju pembagian keuntungan menggunakan perbandingan pengusaha : investor = 2 : 1. Bulan ini, keuntungan bersih bisnis tersebut adalah Rp 90 juta.
Berapakah masing-masing keuntungan yang diterima pengusaha dan investor?
Diketahui:
Keuntungan perusahaan = Rp 90 juta
Pengusaha : investor = 2 : 1
Penyelesaian:
Bentuk perbandingan keuntungan dapat dijadikan menjadi 1 kesatuan, yang diilustrasikan sebagai berikut
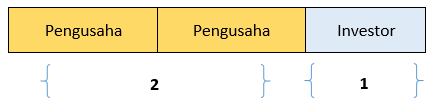
Dari ilustrasi diketahui
Total perbandingan = 2 + 1 = 3
Dalam bentuk pecahan dapat ditulis
Bagian pengusaha = 2/3
Bagian investor = 1/3
Kemudian dapat dihitung
Artikel terkait: Cara Perkalian Pecahan
Jadi, pengusaha mendapat keuntungan Rp 60 juta dan Investor 30 juta dari total keuntungan perusahaan.
D. Jenis-Jenis Perbandingan
Terdapat 2 jenis perbandingan yaitu: perbandingan senilai dan perbandingan berbalik nilai.
D1. Perbandingan Senilai
Perbandingan senilai adalah jenis perbandingan dua atau lebih satuan, saat salah satu nilai meningkat maka nilai lainnya ikut meningkat begitu juga saat salah satu nilai menurun maka nilai lainnya ikut menurun.
Contoh kasus perbandingan senilai:
- Waktu tempuh dan jarak tempuh suatu kendaraan
- Waktu download dan besar file yang di download
- Banyak bahan baku dan banyak produksi barang
- Jumlah pekerja dan jumlah gaji yang dibayarkan perusahaan
- Jumlah hewan ternak dan banyak makanan ternak
Rumus Perbandingan Senilai
Dengan menggunakan konsep pembagian, dapat ditulis
Artikel terkait: Konsep Pembagian dan Cara Pembagian Bersusun
Rumus Menghitung Perbandingan Senilai
Dapat dirumuskan
Contoh: Jumlah pekerja dan jumlah gaji yang dibayarkan
Sebuah rumah dikerjakan oleh 3 pekerja membutuhkan biaya Rp 600.000,00. Untuk meringankan beban pekerja, rumah akan dikerjakan 4 orang. Berapa biaya yang diperlukan untuk membayar pekerja?
Penyelesaian:
Kasus di atas akan dibentuk menjadi perbandingan senilai karena secara logika matematika jika pekerja ditambah, maka gaji bertambah.
# Satuan perbandingan senilai
Dapat dibentuk perbandingan senilai dengan variabel
a = pekerja
b = gaji
# Sehingga dapat dibentuk perbandingan senilai
a1 = jumlah pekerja 3 orang
a2 = jumlah pekerja 4 orang
b1 = Rp 600.000,00
b2 = gaji saat pekerja 4 orang
# Menghitung b2 yaitu gaji saat 4 pekerja
Jadi, jumlah gaji yang dibayarkan saat menggunakan 4 pekerja adalah Rp 800.000,00
D2. Perbandingan Berbalik Nilai
Perbandingan berbalik nilai adalah jenis perbandingan dua atau lebih satuan, saat salah satu nilai meningkat maka nilai lainnya menurun begitu juga saat salah satu nilai menurun maka nilai lainnya meningkat.
Contoh kasus perbandingan berbalik nilai:
- Perbandingan jumlah pekerja dengan waktu untuk menyelesaikan pekerjaan
- Perbandingan kecepatan download dengan waktu untuk mendownload
Rumus Perbandingan Berbalik Nilai
Dengan menggunakan konsep pembagian, dapat ditulis
Artikel terkait: Konsep Perkalian dan Cara Perkalian Bersusun
Rumus Menghitung Berbalik Nilai
Dapat dirumuskan
Contoh: Jumlah pekerja dan waktu untuk menyelesaikan pekerjaan
Seorang kontraktor mempekerjakan 12 orang untuk menyelesaikan bangun jembatan selama 3 bulan. Jika kontraktor tersebut mempekerjakan 18 orang. Berapakah waktu yang diperlukan untuk menyelesaikan jembatan?
Penyelesaian:
Kasus di atas akan dibentuk menjadi perbandingan berbalik nilai karena secara logika matematika jika pekerja ditambah, waktu menyelesaikan pekerjaan berkurang.
# Satuan perbandingan berbalik nilai
Dapat dibentuk perbandingan berbalik nilai dengan variabel
a = pekerja
b = waktu
# Sehingga dapat dibentuk perbandingan senilai
a1 = 12 pekerja
a2 = 18 pekerja
b1 = 3 bulan
b2 = waktu saat 18 pekerja
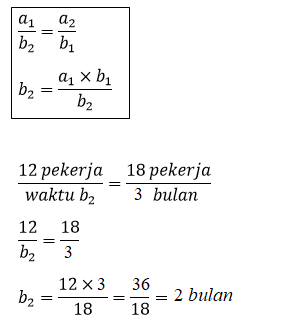
# Menghitung b2 yaitu waktu saat 18 pekerja
Jadi, waktu yang diperlukan menyelesaikan jembatan saat menggunakan 18 pekerja adalah 2 bulan.
Thanks For: Annisa Syahreika Vanesa (Pemeriksa)
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Perbandingan | Rumus Perbandingan, Senilai, Berbalik & Cara Menghitung”. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…


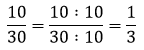

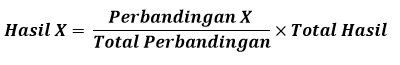


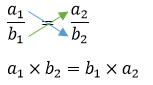
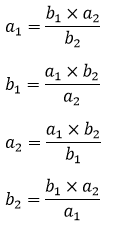


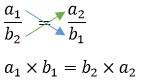
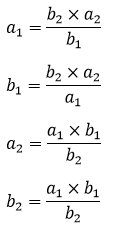










Hi bagaimana cara menghitung dengan soal berikut:
2 unit rumah dikerjakan dengan 4 pekerja dengan waktu 20 hari
berapa pekerja yang dibutuhkan jika ada proyek 5 rumah dengan waktu kerja 40 hari?
Sangat terbantu
Hai, Kak Rahmah Jamilatus Sya'adah
Senang dapat membantu 🙂
min nanya nih,tino pergi suatu ruangan dimana memiliki perbandingan waktu 1 hari di luar ruangan = 100 hari di dalam ruangan.
pertanyaan nya, berapa jumlah waktu di dalam ruangan jika 1 detik di luar ruangan berlalu .
Makasih, saya ahkirnya paham
Senang dapat membantu Kak Alam Sahrambe 🙂