A. Pengertian Perkalian atau Multiplication
Perkalian adalah salah satu operasi aritmatika (operasi dasar matematika) yang berfungsi sebagai simbol operasi penjumlahan berulang. Secara umum simbol operasi perkalian adalah "×" yang disebut dengan "cross sign", untuk mempermudah penulisan operasi perkalian juga dapat disimbolkan dengan tanda "⋅" yang disebut "dot operator". Dalam proses belajar, untuk mempermudah menghitung perkalian biasanya digunakan tabel perkalian 1-10.
Rumus dasar perkalian
a disebut dengan pengali (multiplier)
b disebut dengan bilangan yang dikali (multiplicand)
Contoh:
3 × 2 = 2 + 2 + 2 = 6
Perkalian di atas dibaca "3 kali 2" yang artinya penjumlahan berulang angka 2 sebanyak 3 kali.
2 × 3 = 3 + 3 = 6
Perkalian di atas dibaca "2 kali 3" yang artinya penjumlahan berulang angka 3 sebanyak 2 kali. Walaupun secara matematis menghasilkan nilai yang sama, secara gramatikal kedua bentuk di atas berbeda.
B. Tabel Perkalian 1-10
Berikut tabel perkalian 1-10 untuk mempermudah menghitung perkalian dengan angka yang lebih besar.
Catatan: Geser untuk melihat tabel yang tertutup
| Perkalian 1 | Perkalian 2 | Perkalian 3 | Perkalian 4 | Perkalian 5 |
|---|---|---|---|---|
| 1×1=1 | 1×2=2 | 1×3=3 | 1×4=4 | 1×5=5 |
| 2×1=2 | 2×2=4 | 2×3=6 | 2×4=8 | 2×5=10 |
| 3×1=3 | 3×2=6 | 3×3=9 | 3×4=12 | 3×5=15 |
| 4×1=4 | 4×2=8 | 4×3=12 | 4×4=16 | 4×5=20 |
| 5×1=5 | 5×2=10 | 5×3=15 | 5×4=20 | 5×5=25 |
| 6×1=6 | 6×2=12 | 6×3=18 | 6×4=24 | 6×5=30 |
| 7×1=7 | 7×2=14 | 7×3=21 | 7×4=28 | 7×5=35 |
| 8×1=8 | 8×2=16 | 8×3=24 | 8×4=32 | 8×5=40 |
| 9×1=9 | 9×2=18 | 9×3=27 | 9×4=36 | 9×5=45 |
| 10×1=10 | 10×2=20 | 10×3=30 | 10×4=40 | 10×5=50 |
Catatan: Geser untuk melihat tabel yang tertutup
| Perkalian 6 | Perkalian 7 | Perkalian 8 | Perkalian 9 | Perkalian 10 |
|---|---|---|---|---|
| 1×6=6 | 1×7=7 | 1×8=8 | 1×9=9 | 1×10=10 |
| 2×6=12 | 2×7=14 | 2×8=16 | 2×9=18 | 2×10=20 |
| 3×6=18 | 3×7=21 | 3×8=24 | 3×9=27 | 3×10=30 |
| 4×6=24 | 4×7=28 | 4×8=32 | 4×9=36 | 4×10=40 |
| 5×6=30 | 5×7=35 | 5×8=40 | 5×9=45 | 5×10=50 |
| 6×6=36 | 6×7=42 | 6×8=48 | 6×9=54 | 6×10=60 |
| 7×6=42 | 7×7=49 | 7×8=56 | 7×9=63 | 7×10=70 |
| 8×6=48 | 8×7=56 | 8×8=64 | 8×9=72 | 8×10=80 |
| 9×6=54 | 9×7=63 | 9×8=72 | 9×9=81 | 9×10=90 |
| 10×6=60 | 10×7=70 | 10×8=80 | 10×9=90 | 10×10=100 |
Tips: Perkalian dengan banyak angka 0 berjejer di belakang
Perkalian dengan angka 0 di belakang dapat diselesaikan dengan mengalikan angka di depan nol lalu menambah banyak angka nol di belakang, misalnya:
4000 × 200
= 4 × 2 × 100000
= 8 × 100 000
= 800 000
Terlihat terdapat 5 angka nol di belakang, tanpa menulis uraian di atas kita dapat menjawab pertanyaan tersebut.
C. Cara Menghitung Perkalian
Berikut 2 cara menghitung perkalian yaitu dengan menguraikan dan bersusun.
C1. Menghitung Perkalian dengan Cara Menguraikan
Cara menghitung perkalian dengan menguraikan merupakan cara perkalian dengan mengubah bentuk angka berdasarkan letak satuan, puluhan, ratusan, ribuan, dan seterusnya dengan perkalian satu-satu.
Contoh 1.1: Penguraian sederhana
2 × 123 =
Penyelesaian:
Bilangan yang dikali (multiplicand) diuraikan sebagai
123 = 100 + 20 + 3
Kemudian melakukan perkalian satu-satu terhadap angka 100, 20, 3 yang masing-masing dikali 2 kemudian dijumlahkan.
2 × 123 = 2 × (100 + 20 + 3) = (2×100) + (2×20) + (2×3) = 200 + 40 + 6 = 2 × 123 = 246
Contoh 1.2: Penguraian 2 digit
23 × 45 =
Penyelesaian:
Pengali (multiplier) diuraikan sebagai
23 = 20 + 3
Bilangan yang dikali (multiplicand) diuraikan sebagai
45 = 40 + 5
Kemudian dilanjutkan dengan melakukan perkalian satu-satu.
23 × 45 = (20 + 3) × (40 + 5) = (20×40) + (20×5) + (3×40) + (3×5) = 800 + 100 + 120 + 15 = 1035
Contoh 1.3: Penguraian banyak digit
123 × 789 =
Penyelesaian:
Bilangan yang dikali (multiplicand) diuraikan sebagai
123 = 100 + 20 + 3
Bilangan yang dikali (multiplicand) diuraikan sebagai
789 = 700 + 80 + 9
Kemudian dilanjutkan dengan melakukan perkalian satu-satu.
123 × 789 = (100 + 20 + 3) × (700 + 80 + 9) = (100×700) + (100×80) + (100×9) + (20×700) + (20×80) + (20×9) + (3×700) + (3×80) + (3×9) = 70000 + 8000 + 900 + 14000 + 1600 + 180 + 2100 + 240 + 27 = 97047
C2. Menghitung Perkalian dengan Cara Bersusun
Cara bersusun dapat digunakan untuk mempermudah perhitungan perkalian dengan angka yang besar. Teknik ini berakhir ketika angka terbesar pada bilangan pengali (multiplier) dan bilangan yang dikali (multiplicand) sudah terhitung, lalu ditemukan hasil akhir dengan proses penjumlahan.
Contoh 2.1: Perkalian 1 digit
23 × 9 = 207
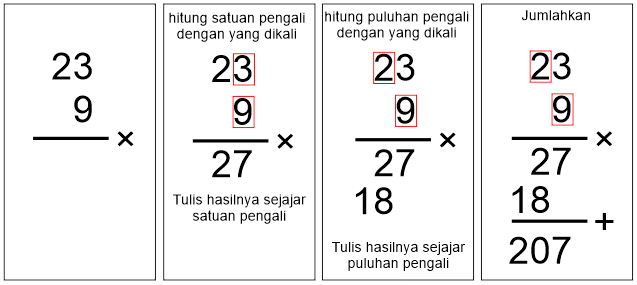
Artikel terkait: Cara Penjumlahan Bilangan dengan Bersusun
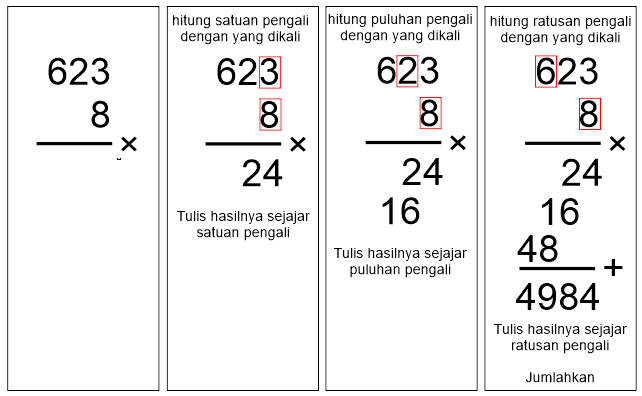
Contoh 2.2: Perkalian 1 digit
623 × 8 = 4984
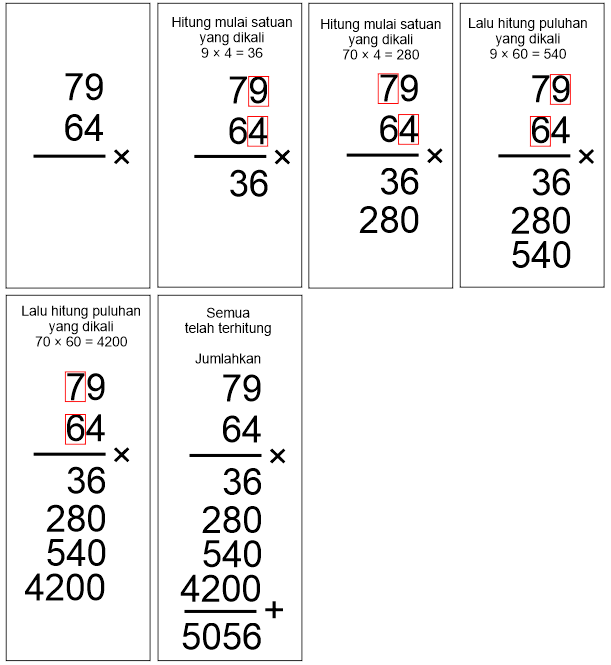
Contoh 2.3: Perkalian banyak digit
79 × 64 = 5056
Untuk menghitung perkalian banyak digit, perlu ditulis angka nol supaya tidak membingungkan saat proses penjumlahan.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Perkalian | Tabel Perkalian 1-10 dan Cara Menghitung Perkalian". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai Fans Page Advernesia. Terima kasih…

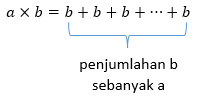













Mks....coba share bhn k email kh...
Hai Matius Yerikho
Avernesia belum mempunyai materi offline yang siap dipublikasikan ke publik
Ini masih menjadi planning 🙂
-90 : 9 X 16 =
yang kaya gini cara gimana???
-90 : 9 X 16 = (-90 : 9 ) X 16
= -10 X 16
= (- 10 X 10) + (-10 X 6)
= ( -100 ) * (-60)
= -160
Tak kah ada
Pengertianya sangat rinci dan mudah dimengerti thx u advernesia
Sama-sama Rifa 🙂