Perkalian aljabar adalah operasi perkalian dengan menggunakan elemen aljabar sebagai operan (objek yang dioperasikan). Sebelum mempelajari perkalian aljabar, diperlukan pemahaman mengenai operasi perkalian pada bilangan dan juga sifat-sifat operasi hitung perkalian (komutatif, asosiatif, dan distributif). Berikut dijelaskan mengenai dasar operasi perkalian aljabar, perkalian aljabar berpangkat, dan perkalian bentuk aljabar.
Navigasi Cepat
- A. Perkalian Aljabar Dasar
- B. Perkalian Aljabar Berpangkat
- Contoh: 4xy × 4xy2
- B1. Perkalian Variabel Berpangkat
- B2. Perpangkatan Variabel Berpangkat
- C. Perkalian Bentuk Aljabar
A. Dasar Perkalian Aljabar
Berikut konsep dasar untuk memahami operasi perkalian aljabar, meliputi (1) perkalian variabel dengan konstanta, (2) perkalian antar variabel, dan (3) perkalian bentuk aljabar dengan konstanta.
Tips: Symbol kali "×" pada operasi aljabar biasanya "tidak ditulis" atau diganti dengan simbol titik "•".
A.1 Perkalian Variabel dengan Konstanta
Cara perkalian variabel dengan konstanta adalah dengan mengali koefisien variabel dengan konstanta yang dikalikan.
ax × b = (a × b)x
Dengan "x" menyatakan variabel; "a" menyatakan koefisien x; dan "b" menyatakan konstanta.
Contoh 1:
3x × 4
= (3 × 4)x
= 12x
Contoh 2:
3y × (-2)
= (3 × (-2))y
= -6y
Contoh 3:
4 × 5 × 7z
= (4 × 5 × 7)z
= 140z
A.2 Perkalian Antar Variabel
Cara perkalian antar variabel adalah dengan menghitung perkalian koefisien lalu dilanjutkan dengan mengali variabel-nya. Perkalian variabel yang sama dapat ditulis dalam bentuk pangkat, misalnya y × y = y2 (dijelaskan pada bagian B).
ax × by = (a × b)xy
Dengan "x & y" menyatakan variabel dan "a & b" menyatakan masing-masing koefisien-nya.
Contoh 1:
x × y × z
= xyz
Contoh 2:
3x × 6y
= (3 × 6)xy
= 18xy
Contoh 3:
2a × 7b
= (2 × 7)ab
= 14ab
Contoh 4:
4x × 3y + 7z
= (4 × 3)xy + 7z
= 12xy + 7z
# Ingat operasi penjumlahan hanya bisa dilakukan saat kedua operan mempunyai variabel yang sama atau sukunya sejenis.
A.3 Perkalian Bentuk Aljabar dengan Konstanta
Cara perkalian bentuk aljabar dengan konstanta adalah dengan menggunakan sifat distributif perkalian untuk memperluas proses perhitungan. Mengingat pelajaran terdahulu mengenai sifat operasi hitung bilangan, berikut 2 konsep dasar sifat distributif perkalian.
# Distributif Perkalian Terhadap Penjumlahan
a × (b + c) = (a × b) + (a × c) = d
# Distributif Perkalian Terhadap Pengurangan
a × (b - c) = (a × b) + (a × (-c)) = e
Tips: Penggabungan nilai negatif terhadap proses perkalian dapat mempermudah perhitungan yang lebih rumit
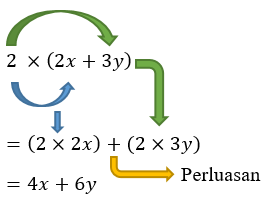
1. Sifat Distributif Perkalian Aljabar Terhadap Penjumlahan
Berikut langkah-langkah cara menyelesaikan operasi perkalian bentuk penjumlahan aljabar dengan konstanta.
Catatan: untuk mempermudah penulisan, operasi 2 × (2x + 3y) dapat ditulis singkat 2 (2x + 3y).
Atau dalam notasi matematika,
2 × (2x + 3y) ⇔ 2 (2x + 3y)
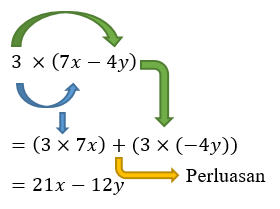
2. Sifat Distributif Perkalian Aljabar Terhadap Pengurangan
Berikut langkah-langkah cara menyelesaikan operasi perkalian bentuk pengurangan aljabar dengan konstanta.
Catatan: untuk mempermudah penulisan, operasi 3 × (7x - 4y) dapat ditulis singkat 3 (7x - 4y).
Atau dalam notasi matematika,
3 × (7x - 4y) ⇔ 3 (7x - 4y)
B. Perkalian Aljabar Berpangkat
Operasi perkalian aljabar dapat menghasilkan bentuk pangkat yang lebih mutakhir. Perkalian aljabar dengan pangkat pada variabel mengikuti sifat perpangkatan, yaitu nilai pangkat dapat dioperasikan terhadap variabel yang sama. Sedangkan koefisien dalam perhitungan dapat dimuat oleh semua hasil dari operasi perkalian. Berikut beberapa cara penyelesaian bentik perkalian aljabar yang dapat menghasilkan bentuk pangkat, yaitu: (1) perkalian aljabar pangkat dan (2) perkalian antar bentuk aljabar.
Baca juga: Cara Menghitung Perpangkatan, Sifat, dan Tabel Perpangkatan
B1. Cara Perkalian Variabel Berpangkat
Dalam konsep dasar perkalian berpangkat, pangkat dapat dijumlahkan apabila bilangan pokoknya sama. Konsep tersebut juga berlaku pada perkalian aljabar, yaitu pangkat tiap variabel yang sama dijumlahkan.
axm × bxn = (a × b)xm + n
Dengan "x" menyatakan variabel; "a & b" menyatakan nilai masing-masing koefisien x; dan "m & n" menyatakan nilai masing-masing pangkat.
Contoh 1:
5z2 × 7z
= 35(z2 × z)
= 35(z2+1)
= 35z3
Contoh 2:
4xy × 4xy2
= 16(xy × xy2)
= 16(x1+1y1+2)
= 16x2y3
Contoh 3:
3z4 × 6z-2
= 18(z4-2)
= 18z2
B2. Perpangkatan Variabel Berpangkat
Sama halnya dalam konsep perpangkatan, pangkat variabel akan dikalikan dan nilai koefisien dipangkatkan biasa.
Contoh 1:
(2x3)2
= 22 x3×2
= 4x6
Contoh 2:
(3x2y3)2
= 32 x2×2 y3×2
= 9x4y6
C. Perkalian Antar Bentuk Aljabar (Algebraic Expressions)
Berdasarkan konsep, perkalian bentuk aljabar dilakukan dengan "perluasan kurung" atau "expansion of brackets" yaitu dengan melakukan perkalian satu-satu tiap suku antar bentuk aljabar di dalam kurung. Langkah ini telah dijelaskan pada bagian A3 untuk kasus yang sederhana. Berikut kasus-kasus yang lebih mutakhir.
C1. Perkalian Bentuk Aljabar dengan Variabel
Cara perhitungan bentuk aljabar dengan variabel yaitu menggunakan sifat distributif.
# Distributif Perkalian Terhadap Penjumlahan
a × (b + c) = (a × b) + (a × c) = d
# Distributif Perkalian Terhadap Pengurangan
a × (b - c) = (a × b) + (a × (-c)) = e ...(i)
yang sama artinya dengan
a × (b - c) = (a × b) - (a × c) = e ...(ii)
Tips: Penggabungan nilai negatif terhadap proses perkalian dapat mempermudah perhitungan yang lebih rumit. Hal ini akan menghasilkan perluasan dengan menggunakan tanda tambah, seperti pada rumus (i).
Contoh 1:
Contoh 2:
C2. Perkalian 2 Bentuk Aljabar Sederhana
Perkalian 2 bentuk aljabar sederhana sering digunakan untuk soal-soal latihan hingga soal yang lebih kompleks. Secara umum, dengan memperluas bentuk menjadi perhitungan satu-satu tiap suku antar bentuk aljabar.
Mengapa hal ini dapat terjadi?
Sebenarnya perluasan di atas berdasarkan sifat distributif pada operasi perkalian, sebagai berikut.
(a + b)(c + d) =
# Pertama, definisikan bentuk (c + d) merupakan sebuah variabel, maka diperoleh
= a (c + d) + b (c + d)
# Berlaku sifat distributif pada bentuk a (c + d) dan b (c + d), diperoleh
= ac + ad + bc + bd
Contoh 1:
(3x + 5y)(4x + 6y)
= 3x.4x + 3x.6y + 5y.4x + 5y.6y
= 12x2 + 18xy + 20xy + 30y2
= 12x2 + (18 + 20)xy + 30y2
= 12x2 + 38xy + 30y2
Contoh 2:
(3x - 2y)(-2x + 6y)
= 3x.(-2x) + 3x.6y + (-2y).(-2x) + (-2y).6y
= -6x2 + (18xy + 4xy) + (-12y2)
= -6x2 + (18 + 4)xy + (-12y2)
= -6x2 + 22xy - 12y2
Contoh 3:
(x + 1)2
= (x + 1)(x + 1)
= x.x + x.1 + 1.x + 1.1
= x2 + x + x + 1
= x2 + (1 + 1)x + 1
= x2 + 2x + 1
C3. Perluasan Kurung Perkalian Bentuk Aljabar (Expansion of Brackets)
Memperluas operasi bentuk aljabar dapat dilakukan dengan melakukan perhitungan distributif setiap kurung, satu-satu dari awal hingga akhir.
a(b + c)(d + e + f)(g + h + i + j) ...
= (ab + ac)(d + e + f)(g + h + i + j)...
= (ab(d + e + f) + ac(d + e + f))(g + h + i + j)...
= (abd + abe + abf + acd + ace + acf)(g + h + i + j) ...
# Garis bawah menunjukkan bentuk yang belum dihitung (hanya untuk memperjelas)
Contoh 1:
3a × (4b + 5c + 6d + 7e)
= 3a.4b + 3a.5c + 3a.6d + 3a.7e
= 12ab + 15ac + 18ad + 21ae
Contoh 2:
(3x + 4y + 5z)(7x + 2y + 3z)
= 3x(7x + 2y + 3z) + 4y(7x + 2y + 3z) + 5z(7x + 2y + 3z)
= (21x2 + 6xy + 9xz) + (28xy + 8y2 + 12yz) + (35xz + 10yz + 15z2)
= 21x2 + 8y2 + 15z2 + (6xy + 28xy) + (9xz + 35xz) + (12yz + 10yz)
= 21x2 + 8y2 + 15z2 + 34xy + 44xz + 22yz
Contoh 3:
(x + y)3
= (x + y)(x + y)(x + y)
= (x.x + x.y + x.y + y.y)(x + y)
= (x2 + 2xy + y2)(x + y)
= x(x2 + 2xy + y2) + y(x2 + 2xy + y2)
= (x3 + 2x2y + xy2) + (x2y + 2xy2 + y3)
= x3 + y3 + (2x2y + x2y) + (xy2 + 2xy2)
= x3 + y3 + 3x2y + 3xy2
Baca juga: Daftar Isi Pelajaran Matematika
Sekian artikel "Perkalian Aljabar, Perkalian Aljabar Berpangkat & Perkalian Bentuk Aljabar". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih ...


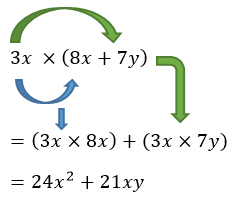
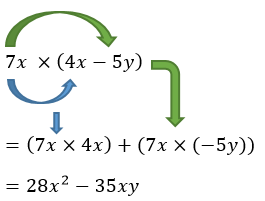
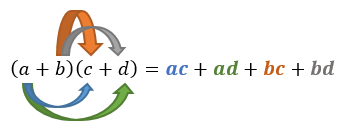










2× (3×+24)
Ayo jawab ka
Ayo ka
gmail nya tidak mau masuk
Hai, Fahri
Sudah dicek, dan email sudah masuk list Newsletter
Terima kasih banyak telah subscribe newsletter Advernesia 🙂