A. Pengertian Bangun Ruang (3D Geometric Shapes)
Bangun ruang adalah bentuk bangun (struktur objek) di ruang 3 dimensi yang dapat diukur bagian-bagiannya dalam koordinat kartesius di R³, yaitu sumbu-x, sumbu-y, dan sumbu-z. Secara sederhana, bangun ruang merupakan objek yang diukur berdasarkan 3 variabel yaitu: panjang (x), lebar (y), dan tinggi (z). Keberadaannya di ruang 3 dimensi menyebabkan bangun ruang mempunyai volume dan luas permukaan. Berikut beberapa hal penting yang perlu diketahui terkait bangun ruang dan rumusnya.
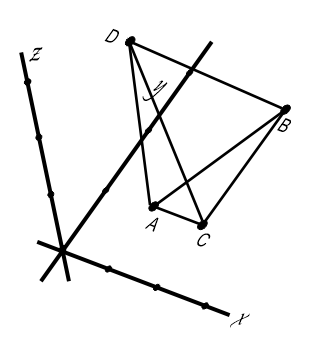
- Bangun ruang dapat diukur melalui koordinat x, y, z di R³ dan memiliki volume, luas permukaan, serta jaring-jaring. Pengukuran bangun ruang menggunakan jarak antar titik di R³. Hal ini diperlukan untuk tingkat pembelajaran yang lebih tinggi terkait geometri analitik.
- Volume bangun ruang adalah banyaknya isi ruang yang digunakan oleh suatu bangun. Satuan yang digunakan yaitu satuan volume, misalnya liter, ml, meter kubik; misalnya dm³ dan cm³.
- Luas permukaan bangun ruang adalah total seluruh luas yang menutupi isi suatu bangun ruang. Luas permukaan suatu bangun ruang ditentukan oleh jaring-jaring-nya. Satuan yang digunakan yaitu satuan luas, misalnya are, hektar, meter kuadrat; misalnya m² dan cm².
- Jaring-jaring bangun ruang adalah bentuk 2-D yang dapat dilipat-lipat hingga membentuk suatu bentuk bangun ruang 3-D. Luas keseluruhan bangun 2-D pada jaring-jaring sama dengan luas permukaan suatu bangun ruang.
- Beberapa bangun ruang, dapat mempunyai definisi ukuran lain. Misalnya, bola mempunyai ukuran diameter yang secara langsung mendefinisikan variabel panjang, lebar, dan tinggi.
Baca juga: Rumus Bangun Datar
B. 8 Jenis dan Rumus Bangun Ruang beserta Contohnya
Berikut jenis-jenis dan rumus bangun ruang yang umum digunakan dalam pembelajaran matematika .Masing-masing contoh soal dapat dibuka melalui tautan yang telah disediakan pada 8 jenis bangun ruang, yaitu: kubus, balok, tabung, kerucut, limas segi tiga, limas segi empat, bola, dan prisma. Untuk mengakses salah satu bangun klik pada navigasi berikut.
Navigasi Cepat
-
Kubus
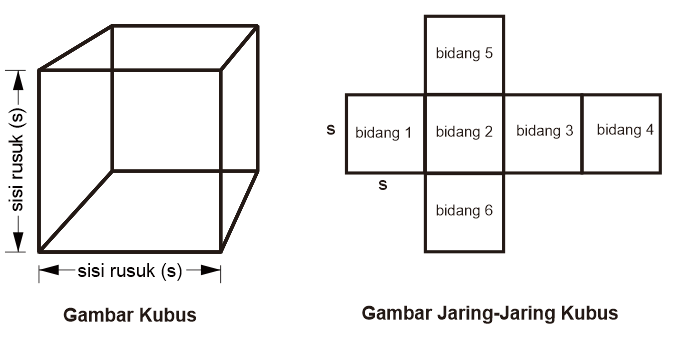
Kubus adalah bangun ruang tiga dimensi yang tersusun dari 6 bidang datar yang kongruen, keenam bidang kongruen pada kubus berbentuk persegi.
Keterangan: s = sisi kubus
Nama Rumus Volume (V) V = s × s × s V = s³ Luas permukaan (L) L = 6 × s × s L = 6 × s² Sisi rusuk (s) Diagonal sisi (ds) Diagonal ruang (dr) Luas bidang diagonal (bd) Artikel terkait: Contoh Soal Kubus
-
Balok
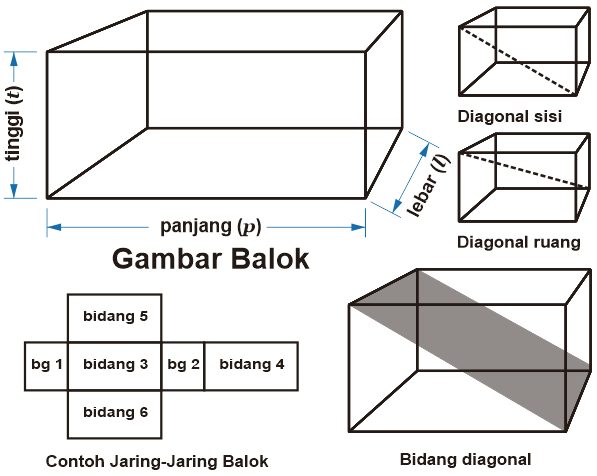
Balok adalah bangun ruang tiga dimensi yang tersusun oleh 3 pasang segi empat (persegi atau persegi panjang) dan paling sedikit mempunyai 1 pasangan sisi segi empat yang mempunyai bentuk yang berbeda.
Keterangan: t = tinggi p = panjang l = lebar
Artikel terkait: Contoh Soal Balok
-
Tabung
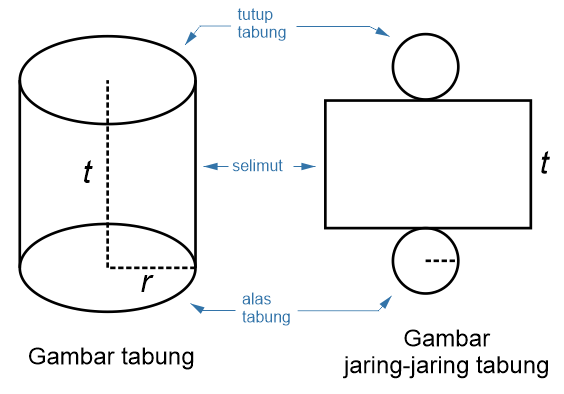
Tabung adalah bangun ruang yang tersusun oleh 3 buah sisi yaitu 2 buah lingkaran yang mempunyai ukuran yang sama dan 1 segiempat yang mengelilingi kedua lingkaran tersebut.
Keterangan: t = tinggi jari-jari (r) = d÷2 diameter (d) = 2×r π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7Artikel terkait: Contoh Soal Tabung
-
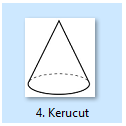
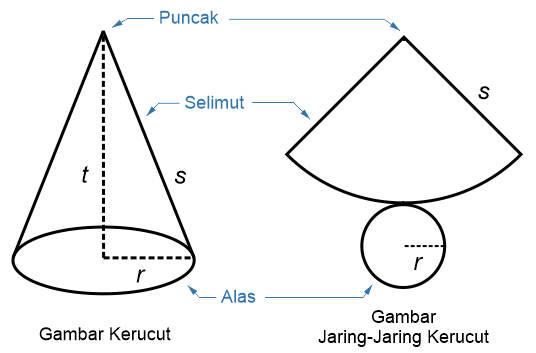
Kerucut
Kerucut adalah bangun ruang yang memiliki 2 sisi yaitu sebuah lingkaran dan sebuah bidang lengkung.
Keterangan: t = tinggi r = jari-jari s = panjang garis pelukis (apotema), merupakan garis yang menghubungkan titik puncak dengan titik keliling alas kerucut. Nilai s dapat dihitung menggunakan rumus Pythagoras.
π = 22/7 untuk jari-jari (r) kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7
Nama Rumus Volume (V) Luas permukaan (L) Luas alas (La) Luas selimut (Ls) Jari-jari (r) diketahui V Jari-jari (r) diketahui L Jari-jari (r) diketahui Ls Tinggi (t) diketahui V Artikel terkait: Contoh Soal Kerucut
-
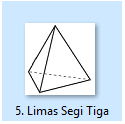
Limas Segitiga
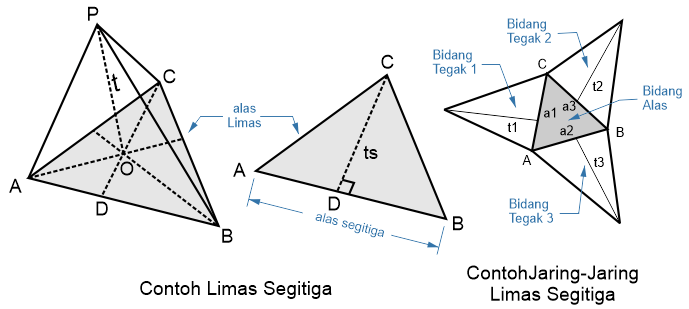
Limas segitiga adalah bangun ruang berjenis limas yang mempunyai sisi alas berbentuk segitiga. Secara umum, Limas adalah jenis bangun ruang yang mempunyai sisi alas berbentuk segi-n dan mengerucut ke satu titik sehingga terbentuk sisi-sisi tegak berbentuk segitiga.
Keterangan: t = tinggi limas (PO) as = alas segitiga (AB) ts = tinggi segitiga alas (DC) t1, t2, t3 = tinggi masing-masing bidang tegak a1, a2, a3 = alas masing-masing bidang tegak
Artikel terkait: Contoh Soal Limas
-
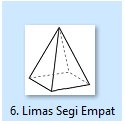
Limas Segiempat
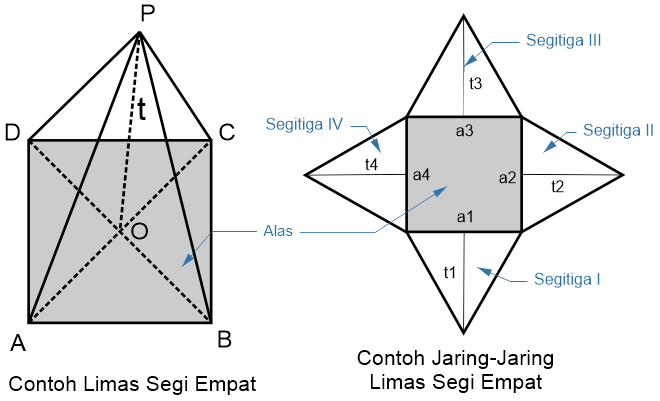
Limas segi empat adalah bangun ruang sejenis limas yang mempunyai alas segi empat (persegi, persegi panjang, belah ketupat, layang-layang, jajar genjang atau trapesium).
Rumus Limas Segi Empat
Nama Rumus Volume (V) V = ⅓ × L alas × t Luas Permukaan (L) L = L alas + L ΔI + L ΔII + L ΔIII + L ΔIV Tinggi t = (3 × V) ÷ L alas Luas Alas Limas Segi Empat
Jenis Alas Luas Alas (La) Alas Persegi La = s × s Alas Persegi Panjang La = p × l Alas Jajar Genjang La = a × t Alas Trapesium Alas Belah Ketupat La = ½ × d1 × d2 Alas Layang-Layang La = ½ × d1 × d2 Luas Sisi Tegak Limas Segi Empat
Sisi Tegak Luas Luas ΔI L ΔI = ½ × a Δ1 × t Δ1 Luas ΔII L ΔII = ½ × a Δ2 × t Δ2 Luas ΔIII L ΔIII = ½ × a Δ3 × t Δ3 Luas ΔIV L ΔIII = ½ × a Δ4 × t Δ4 Artikel terkait: Contoh Soal Limas Segi Empat
-
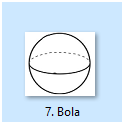
Bola
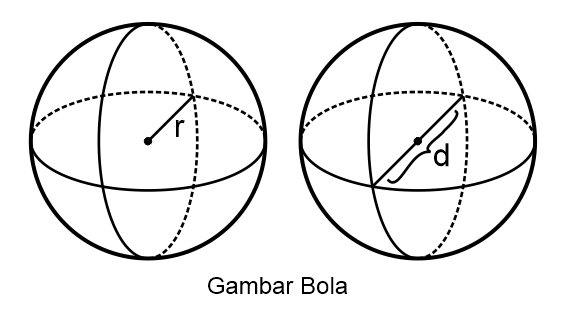
Bola adalah bangun ruang dengan bentuk bulat sempurna yang tersusun oleh tidak terhingga lingkaran yang mempunyai jari-jari dan pusat lingkaran yang sama.
jari-jari (r) = d÷2 diameter (d) = 2×r π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7Nama Rumus Volume (V) V = 4/3 × π × r³ Luas Permukaan (L) L = 4 × π × r² Jari-jari (r) diketahui V Jari-jari (r) diketahui L Artikel terkait: Contoh Soal Bola
-
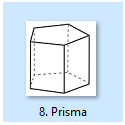
Prisma
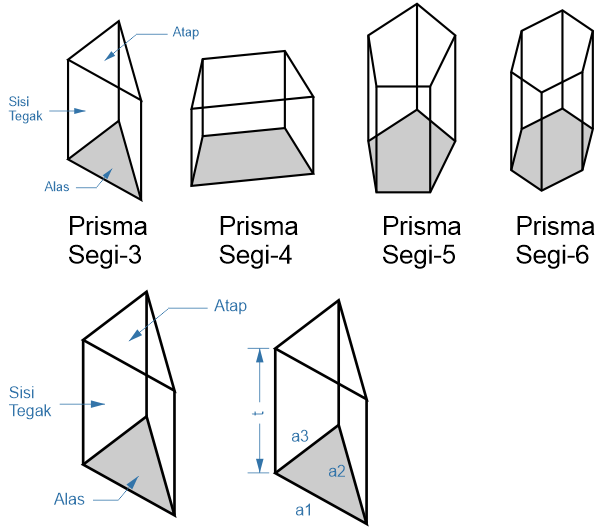
Prisma adalah bangun ruang yang terdiri dari atap dan alas dengan bentuk segi-n yang kongruen beserta dipisahkan oleh sisi-sisi tegak berbentuk segi empat.
t = tinggi prisma La = luas alas
Nama Rumus Volume (V) V = Luas alas × t tinggi (t) jika diketahui V t = V ÷ Luas Alas Luas Permukaan (L) L = t × ( a1 + a2 + ... + an) + (2 × La) L = t × (Keliling Alas) + (2 × La) ∴ Luas Prisma Segi-3 L = t × ( a1 + a2 + a3) + (2 × La) ∴ Luas Prisma Segi-4 L = t × ( a1 + a2 + a3 + a4) + (2 × La) ∴ Luas Prisma Segi-5 L = t × ( a1 + a2 + a3 + a4 + a5) + (2 × La) ∴ Luas Prisma Segi-6 L = t × ( a1 + a2 + a3 + a4 + a5 + a6) + (2 × La) Luas Alas (La) Disesuaikan dengan bentuk prisma Artikel terkait: Contoh Soal Prisma
Untuk contoh soal dan pembahasan untuk masing-masing bangun disediakan pada artikel terkait di bawah tabel rumus.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "8 Rumus Bangun Ruang | Pengertian, Gambar, Volume, Luas, dan Contoh Soal". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...


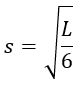
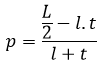
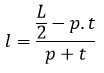
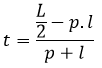
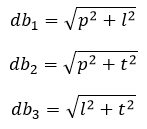
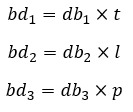
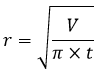
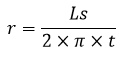
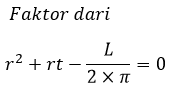
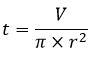
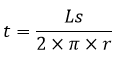
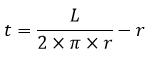
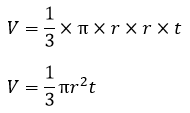
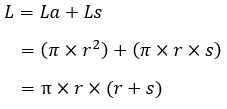
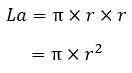
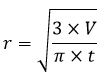
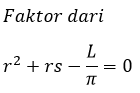
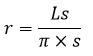
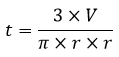
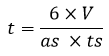
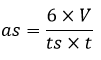
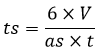
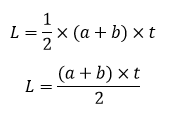
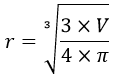
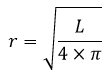










Wadidaw sangat membantu dalam proses pembelajaran
Hai, Dik Kayyisa
Saya sebagai pengelola sangat senang mendengarnya 🙂
Sangat bagus
Hai, Kak Dudi
Terima kasih atas ulasannya
Semoga membantu proses belajarnya 🙂
Semoga halaman ini bermanfat ya ka ..aminn🤲
Hai, Ni Komang RSD
Senang dapat membantu dan semoga bermanfaat, amin 🙂
Terima kasih kak, aku jadi tau tentang volume dan luas permukaan
Hai, Dik Sara
Terima kasih juga atas ulasannya
Senang dapat membantu belajar 🙂
terima kasih banyak kak
Hai, Yasir
Senang dapat membantu belajar matematika 🙂
Bagus & lengkap, sangat membantu sekali🥺 thanks kak
Hai, Rara
Senang dapat membantu belajar matematika
Silakan akses materi lainnya di daftar isi 🙂
Semua bangun datarnya lengkap,rumus ny juga semua lengkap.Makasih kak ☺️☺️
Hai, Dik Tania
Saya sebagai pengelola sangat senang mendengarnya
Setiap bangun datar dan bangun ruang juga mempunyai contoh soal yang dapat diakses melalui daftar isi
Semoga membantu 🙂
Lengkap banget, terima kasih banyak kak😁
Hai, Dzaki
Terima kasih atas ulasannya
Senang dapat membantu 🙂
trimakasih yang takterhingga sangat membantu
Hai, Bu Aini
Senang dapat membantu ibu dalam pekerjaannya 🙂
Sangat membantu banget kak dalam US
Hai, Fahri
Senang dapat membantu belajar Matematika dan juga US 🙂
Uwaa makasii-!Membantu bgt buat US hehe:D
Hai, Octa
Senang dapat membantu Ujian Sekolahnya
Silakan juga melihat materi lainnya 🙂
wah sangat membantu sekali!!!! terima kasih banyak advernesia udh membantu saya untuk menghafalkan rumus2 matematika
Hai, Eka Nuryantie
Senang dapat membantu proses belajar Matematika
Silakan juga membaca materi lainnya di halaman daftar isi, ya 🙂
Kakak bagus materinya. Kaka pengen tau kapan diterbitkannya buat referensi
Hai, Kak Ines
Untuk informasi artikel terkait tanggal terbit, URL, dan pembaruan dapat klik "Tampilkan informasi post" di bagian bawah artikel
Semoga membantu 🙂
Oh ya kak, aku ada pertanyaan itu yang no 8. prisma itu luas permukaannya yang mana ya, yang di atasnya atau dibawahnya ya, soalnya aku masih anak², belum paham banget
Itu sesuai bentuk alasnya dik 🙂
Permisi kak izin copas buat tugas power point adik saya, terima kasiih
Kereeen
Jadi lebih paham
Kereeen
Jadi lebih paham rumusnya
Makasih kak disini semuanya lengkap,semuanya benar sekarang rp ku sudah selesai ,sekarang aku faham rumus nya🤗
Hai, Dik Nisa
Senang dapat membantu belajar matematika 🤗
keren
Hai, Alaina
Senang dapat membantu belajar matematika 🙂
makasi, aku jadi bisa lebih phm tentang rumus rumus inii
Hai, Karina
Terima kasih kembali
Senang dapat membantu belajar matematika 🙂