A. Pengertian Prisma atau Prism
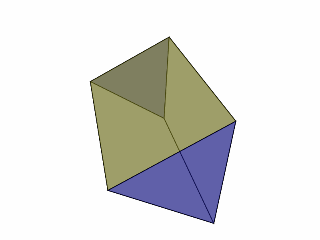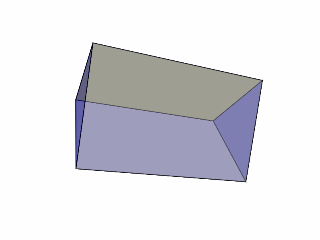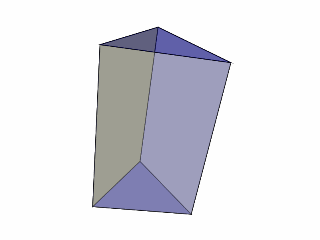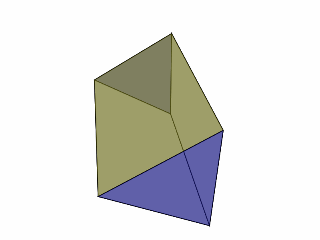
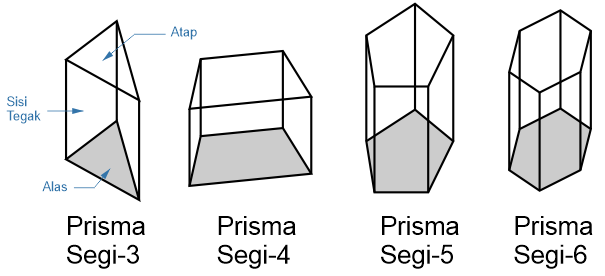
Prisma adalah bangun ruang yang terdiri dari atap dan alas dengan bentuk segi-n yang kongruen beserta dipisahkan oleh sisi-sisi tegak berbentuk segi empat. Sisi atap dan sisi alas prisma bersifat kongruen berarti kedua sisi tersebut mempunyai ukuran dan bentuk yang sama. Bentuk sisi atap dan sisi alas prisma berupa bangun datar segi-n, misalnya segi-3 (prisma segitiga) dan segi-4 (prisma segi empat: prisma trapesium dan prisma jajar genjang). Sebelum mempelajari rumus volume prisma dan luas permukaan prisma sebaiknya kita memahami sifat-sifat prisma.
Artikel terkait: Limas Segitiga | Rumus Volume Limas Segitiga dan Luas Permukaan
B. Sifat-Sifat Prisma
-
Bentuk alas dan atap prisma bersifat kongruen.
-
Alas dan atap prisma berbentuk segi-n, misalnya segitiga dan trapesium.
-
Semua sisi tegak prisma berbentuk segi empat.
-
Jumlah sisi prisma adalah n+2, misalnya:
- Prisma segitiga (n+2=3+2=5 sisi)
- Prisma segi empat (n+2=4+2=6 sisi)
- Prisma segi lima (n+2=5+2=7 sisi)
- Prisma segi enam (n+2=6+2=8 sisi)
-
Jumlah rusuk prisma adalah 3n, misalnya:
- Prisma segitiga (3x3 = 9 rusuk)
- Prisma segi empat (4x3 = 12 rusuk)
- Prisma segi lima (5x3 = 15 rusuk)
- Prisma segi enam (6x3 = 18 rusuk)
-
Jumlah titik sudut prisma adalah 2n, misalnya:
- Prisma segitiga (2×3 = 6 titik sudut)
- Prisma segi empat (2×4 = 8 titik sudut)
- Prisma segi lima (2×5 = 10 titik sudut)
- Prisma segi enam = (2×6 = 12 titik sudut)
C. Rumus Prisma
t = tinggi prisma
La = luas alas
| Nama | Rumus |
|---|---|
| Volume (V) | V = Luas alas × t |
| tinggi (t) jika diketahui V | t = V ÷ Luas Alas |
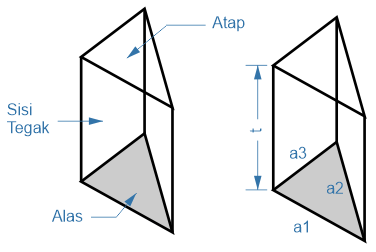
| Luas Permukaan (L) | L = t × ( a1 + a2 + ... + an) + (2 × La) |
| L = t × (Keliling Alas) + (2 × La) | |
| ∴ Luas Prisma Segi-3 | L = t × ( a1 + a2 + a3) + (2 × La) |
| ∴ Luas Prisma Segi-4 | L = t × ( a1 + a2 + a3 + a4) + (2 × La) |
| ∴ Luas Prisma Segi-5 | L = t × ( a1 + a2 + a3 + a4 + a5) + (2 × La) |
| ∴ Luas Prisma Segi-6 | L = t × ( a1 + a2 + a3 + a4 + a5 + a6) + (2 × La) |
| Luas Alas (La) | Disesuaikan dengan bentuk prisma |
Contoh 1: Cara Menghitung Volume Prisma dan Luas Permukaan Prisma
Hitunglah volume prisma dan luas permukaan prisma
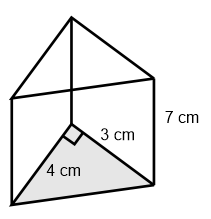
Diketahui:
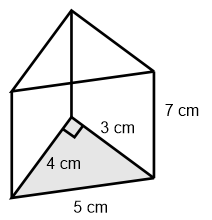
Prisma tersebut merupakan prisma segi-3 dengan bentuk alas segitiga siku-siku
t = 7 cm
* Alas Prisma berbentuk segitiga siku-siku dengan masing-masing sisi tegak
a = 3 cm, dapat disebut alas segitiga
b = 4 cm, dapat disebut tinggi segitiga
Sehingga panjang sisi miring segitiga siku-siku dapat dihitung dengan rumus Pythagoras
Artikel terkait: Rumus Pythagoras Segitiga dan Contoh Soalnya
c = 5 cm, sebagai sisi miring segitiga
Ditanya:
Volume Prisma dan Luas Permukaan Prisma
Penyelesaian:
- Volume Prisma
V = Luas alas × t
Karena alas prisma berbentuk segitiga, dapat dihitung
a = 3 cm, sebagai alas (a) dan b = 4 cm sebagai tinggi (t)
La = ½ × a × t
La = ½ × 3 cm × 4 cm
La = 6 cm²
Sehingga Volume Prisma
V = Luas alas × t
V = 6 cm² × 7 cm
V = 42 cm³
- Luas Permukaan Prisma
Karena alas prisma berbentuk segi-3, sehingga dapat dihitung luas permukaan prisma dengan rumus
L = t × ( a1 + a2 + a3) + (2 × La)
Dari gambar dapat diketahui
Dapat diketahui masing-masing rusuk pada alasnya
a1= 5 cm
a2 =3 cm
a3 = 4 cm
Dengan t = 7 cm
Sehingga luas alasnya
La = ½ × a × t
La = ½ × 3 cm × 4 cm
La = 6 cm²
Kemudian dapat dihitung luas permukaan
L = t × ( a1 + a2 + a3) + (2 × La)
L = 7 cm × ( 5 cm + 3 cm + 4 cm) + (2 × 6 cm²)
L = 84 cm² + 12 cm²
L = 96 cm²
Jadi, volume prisma adalah 42 cm³ dan luas permukaan prisma 96 cm²
Contoh 2: Menghitung Tinggi Prisma
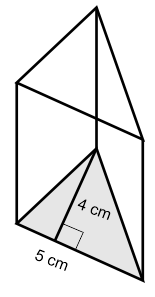
Perhatikan gambar berikut, jika volume prisma 200 cm³. Berapakah tinggi prisma tersebut?
Diketahui:
V = 200 cm³
Alas prisma berbentuk segitiga
Artikel terkait: Rumus Segitiga | Jenis Segitiga, Rumus Luas dan Keliling Segitiga
Ditanya:
Tinggi prisma (t)
Penyelesaian:
t = V ÷ Luas Alas
Sebelumnya harus dihitung luas alas prisma, dari gambar dapat diketahui
Alas berbentuk segitiga dengan
alas segitiga = 5 cm
tinggi segitiga = 4 cm
Sehingga luas alas prisma dapat dihitung dengan rumus luas segitiga
LΔ = ½ × alas segitiga × tinggi segitiga
LΔ = ½ × 5 cm × 4 cm
LΔ = 10 cm²
L alas = 10 cm²
Sehingga diperoleh tinggi
t = V ÷ Luas Alas
t = 200 cm³ ÷ 10 cm²
t = 20 cm
Jadi, tinggi prisma adalah 20 cm.
Animasi Prisma: Pierce, Rod - Math is Fun
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Rumus Prisma | Volume Prisma dan Luas Permukaan Prisma”. Nantikan artikel menarik lainnya dan mohon untuk share dan juga menyukai Fans Page Advernesia. Terima kasih…

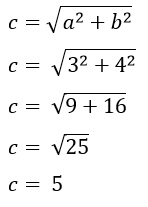






Cara mengetahui luas permukaan prisma hanya dari tinggi prisma gimana kak?
Kak Kira-kira BAB Berikutnya kpn di update ya? Atau cuma smpai sini aja? Btw terima kasih kak sudh membuat materi sprti ini
Hai, Kak Prasatyaade
Advernesia telah membuat beberapa artikel terkait, dapat dilihat di halaman daftar isi
Selain itu Advernesia terus membuat artikel matematika
Semoga membantu 🙂
Saya ingin rumus prisma segi empat yang bentuknya seperti tenda 🙏🏻
Hai, Kak Imrani, Itu namanya Limas bukan Prisma
Jika bentuknya kompleks bisa dilakukan slice bangun tersebut menjadi potongan-potongan
Semoga membantu 🙂